解答题 (共 18 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设二维随机变量 $(X, Y)$ 的联合分布函数
$$
F(x, y)=\left\{\begin{array}{cc}
1-e^{-\lambda_1 x}-e^{-\lambda_2 y}+e^{-\lambda_1 x-\lambda_2 y-\lambda_3 \max \{x, y\}} & \lambda_1, \lambda_2, \lambda_3>0, x>0, y>0 \\
0 & \text { 其它 }
\end{array}\right.
$$
求 $X$ 和 $Y$ 的边缘分布函数.
设随机变量 $X$ 和 $Y$ 的联合分布函数为
$$
F(x, y)=\left\{\begin{array}{cc}
0, & \min \{x, y\} < 0 \\
\min \{x, y\} & 0 \leq \min \{x, y\} < 1 \\
1 & \min \{x, y\} \geq 1
\end{array}\right.
$$
则随机变量 $X$ 的分布函数为
设随机变量 $X$ 为在 $1,2,3,4$ 四个整数中等可能地取一个值,另一个随机变五 $Y$ 在 $1 \sim X$ 中等可能地取一个整数值.试求 $(X, Y)$ 的分布律.
随机变量 $(X, Y)$ 的分布律

$P\{X>1, Y>3\}$ 及 $X$ 和 $Y$ 的边缘分布律.
$(X, Y)$ 的联合分布律为

已知 $P\{Y \leq 0 \mid X < 2\}=0.5$
(1)$a$ 利 $b$ 的值;
(2)在 $X=2$ 条俶下 $Y$ 的条件分布律;
设二维离散型随机变量只取 $(-1,-1),(-1,0),(1,-1),(1,1)$ 四个值,其相应概率 分别为 $\frac{1}{3}, \frac{1}{4}, \frac{1}{6}, \frac{1}{4}$ .
(1)求 $(X, Y)$ 的联合概率分布;
(2)求关于 $X$ 与关于 $Y$ 的边缘概率分布;
(3)求在 $Y=1$ 条件下关于 $X$ 的条件分布与在 $X=1$ 条件下关于 $Y$ 的条件分布.
设二维随机变量 $(X, Y)$ 具有概率密度 $f(x, y)= \begin{cases}2 \mathrm{e}^{-(2 x+y)}, & x>0, y>0, \\ 0, & \text { 其他 }\end{cases}$
(1)求分布函数 $F(x, y)$ ;
(2)求概率 $P\{Y \leq X\}$ .
已知随机变量 $(X, Y)$ 的联合概率密度为
$$
f(x, y)=\left\{\begin{array}{cc}
e^{-y}, & 0 < x < y \\
0, & \text { 其它 }
\end{array}\right.
$$
(1)求 $(X, Y)$ 的联合分价函数
(2)求 $P\{X+Y \leq 1\}$
设随机变量 $X$ 和 $Y$ 具有联合概率密度 $f(x, y)=\left\{\begin{array}{ll}6, & x^2 \leq y \leq x \\ 0, & \text { 其他.}\end{array}\right.$ ,求边缘概率密度 $f_X(x)$ 和 $f_Y(y)$ .
设 $G$ 是平面上的有界区域,其面积 $A$ .若二维随机变量 $(X, Y)$ 具有概率密度
$$
f(x, y)= \begin{cases}\frac{1}{A}, & (x, y) \in G \\ 0, & \text { 其他. }\end{cases}
$$
则称 $(X, Y)$ 在 $G$ 上服从均匀分布.现设二维随机变量在圆域 $x^2+y^2 \leq 1$ 上服从均匀分布,求条件概率密度 $f_{X \mid Y}(x \mid y)$ .
设二维随机变量 $(X, Y)$ 的密度函数为:
$$
f(x, y)=\left\{\begin{array}{cc}
c y(1-x-y), & x>0, y>0, x+y < 1 \\
0, & \text { 其他 }
\end{array}\right.
$$
求(1)常数 $c$ ;
(2)条件:密度函数 $f_{X \mid Y}(x \mid y)$ .
设随机变量 $X \sim\left[\begin{array}{ccc}-1 & 0 & 1 \\ \frac{1}{8} & \frac{1}{2} & \frac{3}{8}\end{array}\right], Y \sim\left[\begin{array}{ccc}-1 & 0 & 1 \\ \frac{3}{8} & \frac{1}{2} & \frac{1}{8}\end{array}\right]$ ,且 $P\{|X| \neq|Y|\}=1$ .
(I)求 $X$ 与 $Y$ 的联合分布律,并讨论 $X$ 与 $Y$ 的独立性;
(II)令 $U=X+Y, V=X-Y$ 讨论 $U$ 与 $V$ 的独立性.
设随机变量 $X, Y$ 相互独立,其概率密度函数分别为
$$
f_X(x)=\left\{\begin{array}{l}
1,0 \leq x \leq 1 \\
0, \text { 其他 }
\end{array}, f_Y(y)=\left\{\begin{array}{l}
e^{-y}, y>0 \\
0, y \leq 0 .
\end{array}\right.\right.
$$
求随机变量 $Z=2 X+Y$ 的概率密度函数.
假设随机变量 $X$ 与 $Y$ 相互独立,如果 $X$ 服从标准正态分布,$Y$ 的概率分布为
$$
P\{Y=-1\}=\frac{1}{4}, \quad P\{Y=1\}=\frac{3}{4}
$$
求 $Z=X Y$ 的概率密度 $f_Z(z)$
若 $X_1, X_2, \cdots, X_n$ 相互独立,且 $X_1 \sim E\left(\lambda_1\right), X_2 \sim E\left(\lambda_2\right), \cdots, X_n \sim E\left(\lambda_n\right)$ ,问 $Z=\min \left\{X_1, X_2, \cdots, X_n\right\}$ 服从什么分布?
假设随机变量 $X$ 与 $Y$ 相互独立,如果 $X$ 服从标准正态分布,$Y$ 的概率分布为
$$
P\{Y=-1\}=\frac{1}{4}, \quad P\{Y=1\}=\frac{3}{4}
$$
求 $Z=|X-Y|$ 的概率密度 $f_Z(z)$ .
在一汽车工厂中,一辆汽车有两道工序是由机器人完成的.其一是紧固 3 只螺栓,其二是焊接 2 处焊点.以 $X$ 表示螺栓紧固得不良的数目,以 $Y$ 表示由机器人焊接的不良焊点的数目.据积累的资料知 $(X, Y)$ 具有分布律:
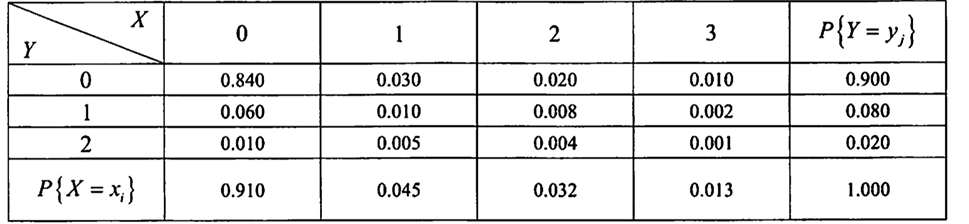
(1)求在 $X=1$ 条件下,$Y$ 的条件分布律;
(2)求在 $Y=0$ 条件下,$X$ 的条件分布律.
设二维连续型随机变量 $(X, Y)$ 在区域 $D=\{(x, y) \mid 0 \leq y \leq x \leq 3-y, y \leq 1\}$ 上服从均匀分布,求边缘密度 $f_X(x)$ 及在 $X=x$ 条件下,关于 $Y$ 的条件概率密度.