单选题 (共 3 题 ),每题只有一个选项正确
设曲线 $y=x \sin x+2 \cos x\left(-\frac{\pi}{2} < x < 2 \pi\right)$ 的拐点为( )。
$\text{A.}$ $(0,2)$
$\text{B.}$ $(\pi,-2)$
$\text{C.}$ $\left(\frac{\pi}{2}, \frac{\pi}{2}\right)$
$\text{D.}$ $\left(\frac{3 \pi}{2},-\frac{3 \pi}{2}\right)$
设函数 $f(x)$ 在 $(-\infty,+\infty)$ 内连续,其导函数的图形如图所示,则
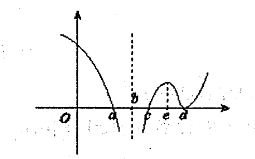
$\text{A.}$ 函数 $f(x)$ 有 2 个极值点,曲线 $y=f(x)$ 有 2 个拐点.
$\text{B.}$ 函数 $f(x)$ 有 2 个极值点,曲线 $y=f(x)$ 有 3 个拐点.
$\text{C.}$ 函数 $f(x)$ 有 3 个极值点,曲线 $y=f(x)$ 有 1 个拐点.
$\text{D.}$ 函数 $f(x)$ 有 3 个极值点,曲线 $y=f(x)$ 有 2 个拐点.
当 $x>0$ 时,曲线 $y=x \sin \frac{1}{x}()$ .
$\text{A.}$ 有且仅有水平渐近线
$\text{B.}$ 有且仅有垂直渐近线
$\text{C.}$ 既有水平渐近线又有垂直渐近线
$\text{D.}$ 既无水平渐近线也无垂直渐近线
填空题 (共 1 题 ),请把答案直接填写在答题纸上
曲线 $y=x \ln \left(e+\frac{1}{x}\right)(x>0)$ 的斜渐近线方程为 $
解答题 (共 13 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
求下列极限.
(1)求 $\lim _{x \rightarrow 0+} x^x$ ;
(2)求 $\lim _{x \rightarrow 1}(2-x)^{\tan \frac{\pi x}{2}}$ .
求下列极限:
(1) $\lim _{x \rightarrow+\infty} \frac{x^n}{e^{\lambda x}}(n$ 为正整数,$\lambda>0)$ ;
(2) $\lim _{x \rightarrow 0^{+}} x^n \ln x(n>0)$ .
求极限 $\lim _{x \rightarrow 0} \frac{2^x-2^{\sin x}}{x^3}$ .
设 $f(x)$ 在 $[0, a]$ 可导,$f(0)=0, f^{\prime}(x)$ 单调递增,讨论 $\varphi(x)=\frac{f(x)}{x}$ 在 $(0, a)$ 内的单调性
当 $0 < a < b < \pi$ 时,证明 $b \sin b+2 \cos b+\pi b>a \sin a+2 \cos a+\pi a$ .
已知 $k>0$ ,讨论方程 $\ln x=k x$ 根的个数.
求函数 $f(x)=2 x^3-3 x^2$ 在 $-1 \leq x \leq 4$ 上的最大值和最小值.
要造一圆柱形油罐,体积为 $V$ ,底半径 $r$ 和高 $h$ 等于多少时,能使表面积最小?此时底直径与高的比是多少?
描绘函数 $y=\frac{x^3}{(x-1)^2}$ 的图形.
曲线 $x^{\frac{2}{3}}+y^{\frac{2}{3}}=1$ 在 $x=\frac{\sqrt{2}}{4}$ 对应点处的曲率为
拋物线 $y=a x^2+b x+c$ 上哪一点处的曲率最大?
某公司总利润 L (万元)与日产量 $q$(吨)之间的函数关系式(即利润函数)为 $L(q)=2 q-0.005 q^2-150$ .试求每天生产 150 吨, 200 吨, 350 吨时的边际利润,并说明经济含义.
设某产品的需求函数为 $Q=Q(P)$ ,收益函数为 $R=P Q$ ,其中 $P$ 为产品价格,$Q$ 为需求量(产品的产量),$Q(P)$ 为单调减函数.如果当价格为 $P_0$ ,对应产量为 $Q_0$ 时,边际收益 $\left.\frac{d R}{d Q}\right|_{Q=Q_0}=a>0$ ,收益对价格的边际效应 $\left.\frac{d R}{d P}\right|_{P=P_0}=c < 0$ ,需求对价格的弹性 $E_P=b>1$ .求 $P_0$ 和 $Q_0$ .
证明题 (共 9 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
若 $f(x)=\ln \cos x$ 是定义在区间 $\left[-\frac{\pi}{3}, \frac{2 \pi}{5}\right]$ 上的函数,证明存在一点 $\xi$ ,使得 $f^{\prime}(\xi)=0$ .
设函数 $f(x)$ 在 $[0,1]$ 上连续,在 0,1 上可导,$f(1)=C$ ,证明:在 0,1 内存在 $\xi$ ,使得 $f^{\prime}(\xi)=-\frac{f(\xi)}{\xi}$.
证明当 $x>0$ 时,$\frac{x}{1+x} < \ln (1+x) < x$ .
$0 < a < b$ ,证明:$\exists \xi \in(a, b)$ ,使得 $a \ln b-b \ln a=\left(a b^2-b a^2\right) \frac{1-\ln \xi}{\xi^2}$ .
设函数 $f(x)$ 在 $[a, b]$ 上连续,在 $[a, b]$ 上可导,且 $f(a)=f(b)=1$ ,证明:$\exists \xi, \eta \in(a, b)$ ,使得 $e^{\eta-\xi}\left[f^{\prime}(\eta)+f(\eta)\right]=1$ 成立.
设 $f(x)$ 在 $[0,1]$ 上连续,在 $(0,1)$ 内可导,证明:在 $(0,1)$ 内至少存在一点 $\xi$ ,使得
$$
f^{\prime}(\xi)=2 \xi[f(1)-f(0)]
$$
求极限 $\lim _{x \rightarrow 0} \frac{e^x-1-x-\frac{x}{2} \sin x}{\sin x-x \cos x}$ .
设函数 $f(x)$ 在 $[0,1]$ 连续,在 $(0,1)$ 内二阶连续可导,证明:至少存在一点 $\xi \in(0,1)$ ,使得 $f\left(\frac{1}{2}\right)=\frac{1}{2} f(0)+\frac{1}{2} f(1)-\frac{1}{8} f^{\prime \prime}(\xi)$
设函数 $f(x)$ 在 $(0,1)$ 内 2 阶可导,且有最大值 1 和最小值 0 ,证明:$\exists \xi \in(0,1)$ ,使得 $f^{\prime \prime}(\xi)>2$ .