单选题 （共 12 题 ），每题只有一个选项正确
已知集合 $A=\{x \mid 0 < x < 4, x \in N\}, B=\{x \mid-3 < x \leq 2, x \in R\}$, 则 $A\cap B=$
$\text{A.}$ $\{x \mid 0 < x \leq 2\}$
$\text{B.}$ $\{x \mid-3 < x < 4\}$
$\text{C.}$ $\{1,2\}$
$\text{D.}$ $\{0,1\}$
设复数 $z$ 满足 $\frac{2+i}{z}=i$, 则 $|z|=$
$\text{A.}$ 1
$\text{B.}$ $\sqrt{5}$
$\text{C.}$ 3
$\text{D.}$ 5
某单位职工参加某APP推出的“二十大知识问答竞赛”活动，参与者每人每天可以作答三次，每次作答20题，每题答对得5分，答错得0分，该单位从职工中随机抽取了10位，他们一天中三次作答的得分情况如图：
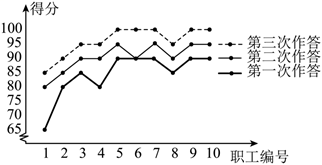
根据图，估计该单位职工答题情况，则下列说法正确的是
$\text{A.}$ 该单位职工一天中各次作答的平均分保持一致
$\text{B.}$ 该单位职工一天中各次作答的正确率保持一致
$\text{C.}$ 该单位职工一天中第三次作答得分的极差小于第二次的极差
$\text{D.}$ 该单位职工一天中第三次作答得分的标准差小于第一次的标准差
如图，网格纸是边长为1的小正方形，在其上用粗线画出了某多面体的三视图，则该多面体的体积为
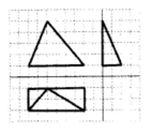
$\text{A.}$ 16
$\text{B.}$ 8
$\text{C.}$ 4
$\text{D.}$ 20
将函数 $f(x)=\sin (2 x+\phi)$ 的图象沿 $x$ 轴向左平移 $\frac{\pi}{8}$ 个单位后, 得到一个偶函数的图象, 则 $\phi$ 的一个可能取值 为
$\text{A.}$ $\frac{\pi}{4}$
$\text{B.}$ $\frac{3 \pi}{8}$
$\text{C.}$ $-\frac{\pi}{4}$
$\text{D.}$ $\frac{3 \pi}{4}$
5 张卡片上分别写有 $0,1,2,3,4$, 若从这 5 张卡片中随机取出 2 张, 则取出的 2 张卡片上的数字之 和大于 5 的概率是
$\text{A.}$ $\frac{1}{10}$
$\text{B.}$ $\frac{1}{5}$
$\text{C.}$ $\frac{3}{10}$
$\text{D.}$ $\frac{4}{5}$
函数 $f(x)=\frac{\left(e^x-1\right) \sin x}{e^x+1}$ 的部分图像大致为
$\text{A.}$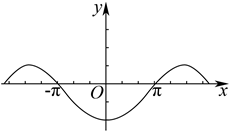 
$\text{B.}$ 
$\text{C.}$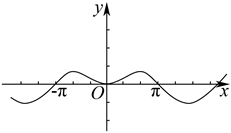 
$\text{D.}$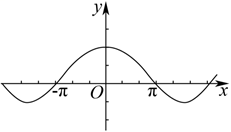 
已知函数 $f(x)=-x^3+3 x^2+9 x+a$ ( $a$ 为常数), 在区间 $[-2,2]$ 上有最大值 20 , 那么此函数在区间 $[-2,2]$ 上的最小值为
$\text{A.}$ -37
$\text{B.}$ -7
$\text{C.}$ -5
$\text{D.}$ -11
如图, 在三棱台 $A B C-A_1 B_1 C_1$ 中, $A A_1 \perp$ 平面 $A B C, \angle A B C=90^{\circ}, A A_1=A_1 B_1=B_1 C_1=1, A B=2$, 则 $A C$ 与平面 $B C C_1 B_1$ 所成的角为
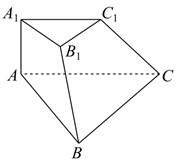
$\text{A.}$ $30^{\circ}$
$\text{B.}$ $45^{\circ}$
$\text{C.}$ $60^{\circ}$
$\text{D.}$ $90^{\circ}$
设甲、乙两个圆柱的底面积分别为 $S_1 、 S_2$, 体积分别为 $V_1 、 V_2$. 若它们的侧面积相等, 且 $\frac{S_1}{S_2}=\frac{9}{4}$, 则 $V_{V_2}$ 的值是
$\text{A.}$ 2
$\text{B.}$ $\frac{3}{2}$
$\text{C.}$ $\frac{4}{3}$
$\text{D.}$ $\frac{5}{4}$
已知椭圆 $E: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的上顶点为 $B$, 右焦点为 $F$, 延长 $B F$ 交椭圆 $E$ 于点 $C$, $A H=\lambda F C(\lambda>1)$, 则椭圆 $E$ 的离心率 $e= $
$\text{A.}$ $\sqrt{\frac{\lambda-1}{\lambda+1}}$
$\text{B.}$ $\frac{\lambda-1}{\lambda+1}$
$\text{C.}$ $\sqrt{\frac{\lambda^2-1}{\lambda^2+1}}$
$\text{D.}$ $\frac{\lambda^2-1}{\lambda^2+1}$
已知 $a=\ln 1.1, b=\frac{1}{11}, c=\sqrt{0.1}$, 则
$\text{A.}$ $a>b>c$
$\text{B.}$ $a>c>b$
$\text{C.}$ $c>b>a$
$\text{D.}$ $c>a>b$
填空题 （共 4 题 ），请把答案直接填写在答题纸上
已知向量 $\vec{a}=(1,2)$, 向量 $\vec{b}=(3, t)$, 若 $(\vec{a}+\vec{b}) \perp \vec{a}$, 则 $t=$
若直线 $3 x-4 y+12=0$ 与两坐标轴交点为 $A, B$, 则以线段 $A B$ 为直径的圆的方程是
已知直线 $y=\sqrt{2} x$ 与双曲线 $x^2-\frac{y^2}{b^2}=1(b>0)$ 无交点, 则该双曲线离心率的最大值为
在三角形 $A B C$ 中, 角 $A, B, C$ 所对的边分别为 $a, b, c$, 若 $\frac{\sin A}{a}=\frac{\sqrt{3} \cos B}{b}=\frac{\sqrt{2}}{2}$, 则该三角形周长的最 大值为
解答题 （共 7 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
安全正点、快捷舒适、绿色环保的高速铁路越来越受到中国人民的青睐．为了解动车的终到正点率，某调查中心分别随机调查了甲、乙两家公司生产的动车的300个车次的终到正点率，得到如下列联表：
(1)根据上表, 分别估计这两家公司生产的动车的终到正点率不低于 0.95 的概率;
(2)能否有 $90 \%$ 的把握认为甲、乙两家公司生产的动车的终到正点率是否低于 0.95 与生产动车的公司有 关?
附: $K^2=\frac{n(a d-b c)^2}{(a+b)(c+d)(a+c)(b+d)}$.
已知数列 $\{a n\}$ 满足 $a _{n+1}=\frac{6 a_n-4}{a_n+2}$, 且 $a_l=3\left(n \in \mathbf{N}^*\right)$.
(1)证明：数列 $\left\{\frac{1}{a_n-2}\right\}$ 是等差数列;
(2)求数列 $\{a_n\}$ 的通项公式.
如图, 在四棱雉 $P-A B C D$ 中, 底面 $A B C D$ 为直角梯形, $\angle B A D=\angle C B A=\frac{\pi}{2}, P A=A D=$ $D P=A B=2, B C=1$, 平面 $P A D \perp$ 平面 $A B C D, M$ 为 $P D$ 的中点.
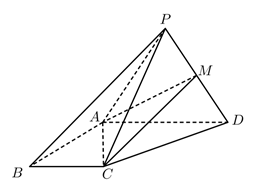
(1)证明: $C M \|$ 平面 $P A B$;
(2)求多面体 $P A B C M$ 的体积.
（1）已知函数 $f(x)=\frac{e^x}{x^2+1}$, 求 $f^{\prime}(1)$;
(2) 已知函数 $g(x)=x^3+a x$, 若曲线 $g(x)$ 在 $x=0$ 处的切线也与曲线 $h(x)=-\ln x$ 相切, 求 $a$ 的值.
设抛物线 $C: y^2=2 p x(p>0)$ 的焦点为 $F$, 过 $F$ 的直线交 $C$ 于 $M, N$ 两点, $|M N|_{\min }=4$.
(1)求 $C$ 的方程;
(2)设点 $D(2 p, 0)$, 直线 $M D, N D$ 与 $C$ 的另一个交点分别为 $A, B$, 当直线 $M N, A B$ 的斜率存在时, 分别记为
$k_1, k_2$. 则 $\frac{k_1}{k_2}$ 是否为常数, 请说明理由.
极坐标系, 曲线 $C_2$ 的极坐标方程为 $\rho^2+2 \rho \cos \theta-4=0$.
(1) 把 $C_1$ 的参数方程化为极坐标方程;
(2) 求 $C_1$ 与 $C_2$ 交点的极坐标 $(\rho \geq 0,0 \leq \theta < 2 \pi)$.
若 $a, b, c \in \mathbf{R}_{+}$, 且满足 $a+b+c=2$.
(1) 求 $a b c$ 的最大值;
(2) 证明: $\frac{1}{a}+\frac{1}{b}+\frac{1}{c} \geq \frac{9}{2}$.