单选题 (共 8 题 ),每题只有一个选项正确
已知集合 $A=\{-1,0,1\}, B=\{0,1,4\}$ ,则 $A \cap B=()$
$\text{A.}$ $\{0\}$
$\text{B.}$ $\{1\}$
$\text{C.}$ $\{0,1\}$
$\text{D.}$ $\{-1,0,1,4\}$
函数 $f(x)=\cos \left(x+\frac{\pi}{4}\right)$ 的最小正周期是()
$\text{A.}$ $\frac{\pi}{4}$
$\text{B.}$ $\frac{\pi}{2}$
$\text{C.}$ $\pi$
$\text{D.}$ $2 \pi$
$|2-4 i|=$
$\text{A.}$ 2
$\text{B.}$ 4
$\text{C.}$ $2 \sqrt{5}$
$\text{D.}$ 6
已知向量 $\vec{a}=(0,1), \vec{b}=(1,0)$ ,则 $\vec{a} \cdot(\vec{a}-\vec{b})=$
$\text{A.}$ 2
$\text{B.}$ 1
$\text{C.}$ 0
$\text{D.}$ -1
双曲线 $x^2-\frac{y^2}{9}=1$ 的浙近线方程为
$\text{A.}$ $y= \pm x$
$\text{B.}$ $y=+2 x$
$\text{C.}$ $y= \pm 3 x$
$\text{D.}$ $y= \pm 4 x$
底面直径和母线长均为 2 的圆锥的体积为()
$\text{A.}$ $\frac{\sqrt{3}}{3} \pi$
$\text{B.}$ $\pi$
$\text{C.}$ $2 \pi$
$\text{D.}$ $3 \pi$
在 $\triangle A B C$ 中,$B C=8, A C=10, \cos \angle B A C=\frac{3}{5}$ ,则 $\triangle A B C$ 的面积为()
$\text{A.}$ 6
$\text{B.}$ 8
$\text{C.}$ 24
$\text{D.}$ 48
已知函数 $f(x)=x|x-a|-2 a^2$ ,若当 $x>2$ 时,$f(x)>0$ ,则 $a$ 的取值范围是()
$\text{A.}$ $(-\infty, 1]$
$\text{B.}$ $[-2,1]$
$\text{C.}$ $[-1,2]$
$\text{D.}$ $[-1,+\infty)$
多选题 (共 3 题 ),每题有多个选项正确
已知 $F(2,0)$ 是抛物线 $C: y^2=2 p x$ 的焦点,$M$ 是 $C$ 上的点,$O$ 为坐标原点.则()
$\text{A.}$ $p=4$
$\text{B.}$ $|M F| \geq|O F|$
$\text{C.}$ 以 $M$ 为圆心且过 $F$ 的圆与 $C$ 的准线相切
$\text{D.}$ 当 $\angle O F M=120^{\circ}$ 时,$\triangle O F M$ 的面积为 $2 \sqrt{3}$
在人工神经网络中,单个神经元输入与输出的函数关系可以称为激励函数.双曲正切函数是一种激励函数.定义双曲正弦函数 $\sinh x=\frac{ e ^x- e ^{-x}}{2}$ ,双曲余弦函数 $\cosh x=\frac{ e ^x+ e ^{-x}}{2}$ ,双曲正切函数 $\tanh x=\frac{\sinh x}{\cosh x}$ .则
$\text{A.}$ 双曲正弦函数是增函数
$\text{B.}$ 双曲余弦函数是增函数
$\text{C.}$ 双曲正切函数是增函数
$\text{D.}$ $\tanh (x+y)=\frac{\tanh x+\tanh y}{1+\tanh x \tanh y}$
填空题 (共 3 题 ),请把答案直接填写在答题纸上
已知函 $f(x)=a^x(a>0, a \neq 1)$ ,若 $f(\ln 2) f(\ln 4)=8$ ,则 $a=$
有 8 张卡片,分别标有数字 $1,2,3,4,5,6,7,8$ ,现从这 8 张卡片中随机抽出 3 张,则抽出的 3张卡片上的数字之和与其余 5 张卡片上的数字之和相等的概率为
已知曲线 $C: y=x^3-\frac{2}{x}$ ,两条直线 $l_1, ~ l_2$ 均过坐标原点 $O, l_1$ 和 $C$ 交于 $M, ~ N$ 两点,$l_2$ 和 $C$ 交于 $P, ~ Q$两点,若三角形 $\triangle O P M$ 的面积为 $\sqrt{2}$ ,则三角形 $\triangle M N Q$ 的面积为
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
为考察某种药物 A 对预防疾病 $B$ 的效果,进行了动物(单位:只)试验,得到如下列联表:
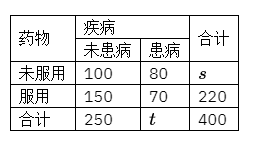
(1)求 $s, t$ ;
(2)记未服用药物 A 的动物患疾病 $B$ 的概率为 $P$ ,给出 $P$ 的估计值;
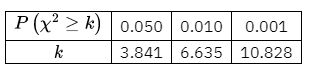
(3)根据小概率值 $\alpha=0.01$ 的独立性检验,能否认为药物 A 对预防疾病 $B$ 有效?
附:$\chi^2=\frac{n(a d-b c)^2}{(a+b)(c+d)(a+c)(b+d)}$ ,
已知数列 $\left\{a_n\right\}$ 中,$a_1=3, a_{n+1}=\frac{3 a_n}{a_n+2}$
(1)证明:数列 $\left\{1-\frac{1}{a_n}\right\}$ 为等比数列;
(2)求 $\left\{a_n\right\}$ 的通项公式;
(3)令 $b_n=\frac{a_{n+1}}{a_n}$ ,证明:$b_n < b_{n+1} < 1$ .
已知函数 $f(x)=a \ln x+\frac{b}{x}-x$ .
(1)设 $a=1, b=-2$ ,求曲线 $y=f(x)$ 的斜率为 2 的切线方程;
(2)若 $x=1$ 是 $f(x)$ 的极小值点,求 $b$ 的取值范围.
已知椭圆 $C$ 的离心率为 $\frac{1}{2}$ ,左,右焦点分别为 $F_1(-1,0), F_2(1,0)$
(1)求 $C$ 的方程;
(2)已知点 $M_0(1,4)$ ,证明:线段 $F_1 M_0$ 的垂直平分线与 $C$ 恰有一个公共点;
(3)设 $M$ 是坐标平面上的动点,且线段 $F_1 M$ 的垂直平分线与 $C$ 恰有一个公共点,证明 $M$ 的轨迹为圆,并求该圆的方程.
在平面四边形 $A B C D$ 中,$A B=A C=C D=1, \angle A D C=30^{\circ}, \angle D A B=120^{\circ}$ ,将 $\triangle A C D$ 沿 $A C$ 翻折至 $\triangle A C P$ ,其中 $P$ 为动点.
(1)设 $P C \perp A B$ ,三棱锥 $P-A B C$ 的各个顶点都在球 $O$ 的球面上.
(i)证明:平面 $P A C \perp$ 平面 $A B C$ ;
(ii)求球 $O$ 的半径
(2)求二面角 $A-C P-B$ 的余弦值的最小值.