单选题 (共 8 题 ),每题只有一个选项正确
已知集合 $A=\{1,2,3,4,5\}, B=\left\{x \left\lvert\, \frac{x-1}{2} \in Z \right.\right\}$ ,则 $A \cap B=$
$\text{A.}$ $\{5\}$
$\text{B.}$ $\{3,5\}$
$\text{C.}$ $\{1,3,5\}$
$\text{D.}$ $\{2,4\}$
已知向量 $\vec{a}=(3,1), \vec{b}=(-2, x)$ ,若 $\vec{a} \perp(\vec{a}+\vec{b})$ ,则 $|\vec{b}|=$
$\text{A.}$ 2
$\text{B.}$ 3
$\text{C.}$ $2 \sqrt{5}$
$\text{D.}$ $\frac{2 \sqrt{10}}{3}$
底面积是 $\pi$ ,侧面积是 $3 \pi$ 的圆锥的体积是
$\text{A.}$ $2 \sqrt{2} \pi$
$\text{B.}$ $\sqrt{2} \pi$
$\text{C.}$ $\frac{2 \pi}{3}$
$\text{D.}$ $\frac{2 \sqrt{2} \pi}{3}$
某电视台举行主持人大赛,每场比赛都有 17 位专业评审进行现场评分,首先这 17 位评审给出某位选手的原始分数,评定该位选手的成绩时从 17 个原始成绩中去掉一个最高分,一个最低分,得到 15 个有效评分,则 15 个有效评分与 17 个原始评分相比,在数字特征"(1)中位数(2)平均数(3)方差(4)极差"中,可
能变化的有
$\text{A.}$ 4 个
$\text{B.}$ 3 个
$\text{C.}$ 2 个
$\text{D.}$ 1 个
已知点 $A(0,1), B(2 \sqrt{3}, 1)$ ,动点 $P$ 满足 $\angle A P B=120^{\circ}$ ,若点 $P$ 的轨迹与直线 $y=\frac{\sqrt{3}}{3} x+b$ 有两个公共点,则 $b$ 的值可以是
$\text{A.}$ $\frac{\sqrt{3}}{3}+1$
$\text{B.}$ $-\frac{4}{5}$
$\text{C.}$ $\frac{6}{5}$
$\text{D.}$ $\frac{4 \sqrt{3}}{3}-1$
若正六棱锥 $P-A B C D E F$ 的体积为 $8 \sqrt{3}$ ,则 $P A$ 的最小值为
$\text{A.}$ $2 \sqrt{3}$
$\text{B.}$ 3
$\text{C.}$ 4
$\text{D.}$ $3 \sqrt{2}$
已知双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的左,右焦点分别为 $F_1, F_2, P$ 是双曲线 $C$ 上位于第一象限的一点,且 $\angle F_1 P F_2=90^{\circ}$ ,设 $O$ 为坐标原点,$N$ 为 $P F_2$ 的中点,$\angle F_1 P F_2$ 的角平分线交线段 $O N$ 于点 $M$ ,若 $|O M|=|M N|$ ,则双曲线 $C$ 的离心率为
$\text{A.}$ $\sqrt{2}$
$\text{B.}$ 2
$\text{C.}$ $\sqrt{5}$
$\text{D.}$ 3
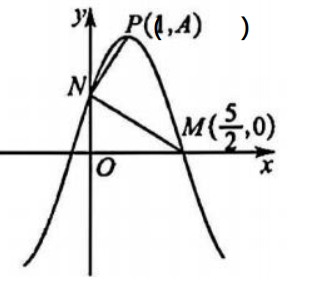
已知函数 $f(x)= A \sin (\omega x+\varphi)\left( A >0, \omega>0,|\varphi| < \frac{\pi}{2}\right)$ 的图象如图所示,图象与 $x$ 轴的交点为 $M\left(\frac{5}{2}, 0\right)$ ,与 $x$ 轴的交点为 $N$ ,最高点 $P(1, A)$ ,且满足 $N M \perp N P$ ,若将 $f(x)$ 的图象向左平移 1 个单位得到 $g (x)$ 的图象,则 $g (2024)=$
$\text{A.}$ $-\frac{\sqrt{10}}{2}$
$\text{B.}$ 0
$\text{C.}$ $\frac{\sqrt{10}}{2}$
$\text{D.}$ $\sqrt{10}$
多选题 (共 3 题 ),每题有多个选项正确
已知 $m, n$ 是两条不相同的直线,$\alpha, \beta$ 是两个不重合的平面,则下列命题为真命题的是
$\text{A.}$ 若 $m, n$ 是异面直线,$m \subset \alpha, m / / \beta, n \subset \beta, n / / \alpha$ ,则 $\alpha / / \beta$
$\text{B.}$ 若 $m \perp n, m \perp \beta$ ,则 $n / / \beta$
$\text{C.}$ 若 $n / / \alpha, n \perp \beta$ ,则 $\alpha \perp \beta$
$\text{D.}$ 若 $m \perp \alpha, n / / \beta, \alpha / / \beta$ ,则 $m \perp n$
已知函数 $f(x)=\sin \omega x-\sqrt{3} \cos \omega x(\omega>0)$ 在 $[0,2 \pi]$ 上恰有 3 个零点,则
$\text{A.}$ $\frac{7}{6} \leq \omega \leq \frac{5}{3}$
$\text{B.}$ $f(x)$ 在 $\left[\frac{5 \pi}{7}, \frac{11 \pi}{10}\right]$ 上单调递减
$\text{C.}$ 函数 $g(x)=f(x)-\sqrt{2}$ 在 $\left[\frac{\pi}{2}, 2 \pi\right]$ 上最多有 3 个零点
$\text{D.}$ $f(x)$ 在 $\left[\frac{\pi}{2}, 2 \pi\right]$ 上恰有 2 个极值点
已 知 定义在 $R$ 上的函数 $f(x), g(x)$ 的导函数分别为 $f^{\prime}(x), g^{\prime}(x)$ ,且 $f(x)=f(4-x)$ , $f(1+x)-g(x)=4, f^{\prime}(x)+g^{\prime}(1+x)=0$ ,则
$\text{A.}$ $g(x)$ 关于直线 $x=1$ 对称
$\text{B.}$ $g^{\prime}(3)=1$
$\text{C.}$ $f^{\prime}(x)$ 的周期为 4
$\text{D.}$ $f^{\prime}(n) \cdot g^{\prime}(n)=0(n \in Z )$
填空题 (共 3 题 ),请把答案直接填写在答题纸上
已知数列 $\left\{a_n\right\}$ 满足 $a_{n+1}^2=a_n a_{n+2}$ ,若 $a_1=\frac{1}{2}, a_4=4$ ,则 $S_4=$
$(x+3 \sqrt{x}+2)^4$ 的展开式中,含 $x$ 的项的系数为
已知抛物线 $y^2=2 p x(p>0)$ 的焦点为 $F(2,0)$ ,过点 $C(-2,0)$ 的直线 $l$ 与抛物线交于 $A, B$ 两点,且 $x_A>x_B$ ,若 $B F$ 为 $\triangle A F C$ 的角平分线,则直线 $l$ 的斜率为
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在 $\triangle A B C$ 中,角 $A, B, C$ 的对边分别为 $a, b, c, b \sin 2 C=c \sin B, V A B C$ 的外接圆半径为 $\frac{2 \sqrt{3}}{3}$ ,
(1)求角 $C$ :
(2)若 $\triangle A B C$ 的面积为 $4 \sqrt{3}$ ,求 $\triangle A B C$ 的周长.
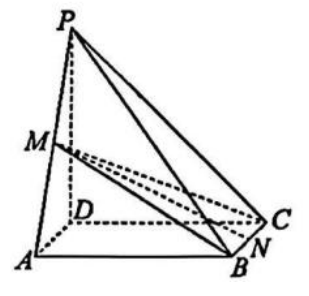
如图,在四棱锥 $P-A B C D$ 中,底面 $A B C D$ 是矩形,$M$ 是 $P A$ 的中点,$N$ 是 $B C$ 的中点,$P D \perp$ 平面 $A B C D$ ,且 $P D=C D=4, A D=2$ .
(1)求证:$M N / /$ 平面 $P C D$ ;
(2)求 $A P$ 与平面 $C M B$ 所成角的正弦值;
(3)求二面角 $M-C B-P$ 的余弦值.
已知 $a>0$ ,函数 $f(x)=\frac{ e ^x(a x-1)}{x-1}$ .
(1)若 $a=2$ ,求 $f(x)$ 的单调区间;
(2)若 $f(x)$ 在 $(2,+\infty)$ 上不单调,求 $a$ 的取值范围.
已知圆 $O: x^2+y^2=1$ 和点 $M(1, \sqrt{3})$ .
(1)过点 $M$ 作圆 $O$ 的切线,求切线的方程;
(2)已知 $A(2,4)$ ,设 $P$ 为满足方程 $|P A|^2+|P O|^2=34$ 的任意一点,过点 $P$ 向圆 $O$ 引切线,切点为 $B$ ,试探究:平面内是否存在一定点 $N$ ,使得 $\frac{|P B|^2}{|P N|^2}$ 为定值?若存在,则求出定点 $N$ 的坐标,并指出相应的定值:若不存在,则说明理由;
(3)过点 $M$ 作直线 $l$ 交圆 $O$ 于两个不同的点 $C, D$( 线段 $C D$ 不经过圆心 $O$ ),分别在点 $C, D$ 处作圆 $O$ 的切线,两条切线交于点 $E$ ,求证:点 $E$ 在一条定直线上,并求出该直线的方程.
一游戏规则如下:一个质点在数轴上运动,从原点出发,每次向左或者向右移动一个单位,共移动了 $n$ 次.
(1)已知质点每次向右移动的概率为 $p(0 < p < 1)$ .
① 当 $p=\frac{1}{2}, n=6$ 时,求质点最终回到原点的樫率;
② 规定质点在运动过程中,只要出现在原点左侧,游戏就结束,否则游戏就继续,直到移动了 $n$ 次,分别求出当 $n=3$ 和 $n=5$ 时质点最终落在原点右侧的概率并比较它们的大小
(2)现在规定游戏分为两个阶段:第一阶段,质点每次向右移动的概率为 $p_1$ ,共移动了 3 次,若质点最终落在了原点左侧,则结束游戏,且最终得分为 0 分.若最终落在了原点右侧,则通过第一阶段,并进入第二阶段:质点重新回到原点,每次向右移动的概率为 $p_2$ ,并再次移动了 3 次,若质点最终落在了原点左侧,则最终得分也为 0 分;若最终落在了原点右侧,则最终得分为质点位于数轴上所在位置对应的实数.
① 请用含 $p_1, p_2$ 的式子表示该游戏得分的数学期望;
② 若 $p_1+p_2=1$ ,则当 $p_1$ 取何值的时候,该游戏得分的期望值最大?