解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
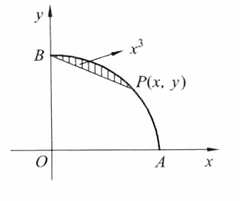
设曲线 $y=f(x)$ 为连结 $A(1,0)$ 与 $B(0,1)$ 两点的弧段且位于弦 $A B$ 的上方(见下图), $P(x, y)$ 为其上任意一点,弦 $B P$ 与该曲线围成的面积为 $x^3$ ,试求该曲线方程。
设对任意 $x>0$ ,曲线 $y=f(x)$ 上点 $(x, f(x))$ 处的切线在 $y$ 轴上的截距等于 $\frac{1}{x} \int_0^x f(t) d t$ ,求 $f(x)$ .
设 $y(x)(x \geqslant 0)$ 二阶可导,且 $y^{\prime}(x)>0, y(0)=1$ .过 $y=y(x)$ 上任意一点 $P(x, y)$ 作该曲线的切线及 $x$ 轴的垂线,上述两直线与 $x$ 轴所围三角形的面积记为 $S_1$ ,区间 $[0, x]$ 上以 $y=y(x)$ 为曲边的曲边梯形面积记为 $S_2$ ,且 $2 S_1-S_2=1$ ,求 $y(x)$ .
一半球体的雪堆,其体积融化的速度与半球表面积 $S$ 成正比,比例系数 $k>0$ .设在融化过程中雪堆始终保持半球形状,设半径为 $r_0$ 的雪堆在开始融化 3 小时内融化其体积的 $\frac{7}{8}$ ,问雪堆全部融化需要多少小时?
某湖泊水量为 $V$ ,每年排人湖泊内含污染物 $A$ 的污水量为 $\frac{V}{6}$ ,流人湖泊内不含污染物 $A$ 的水量为 $\frac{V}{6}$ ,流出湖泊的水量为 $\frac{V}{3}$ .设 1999 年湖泊中污染物 $A$ 的含量为 $5 m_0$ ,严重超过国家标准,为治理污染,从 2000 年起,限制排人湖泊中含 $A$ 污水浓度不超过 $\frac{m_0}{V}$ ,问需要多少年,湖泊中 $A$ 的含量才降到 $m_0$ 内?
某种飞机在机场降落时,为了减少滑行距离,在触地的瞬间,飞机尾部张开减速伞,以增大阻力,使飞机迅速减速并停下来.现有一质量为 9000 kg 的飞机,着陆时的水平速度为 $700 km / h$ .经测试,减速伞打开后,飞机所受的总阻力与飞机的速度成正比(比例系数为 $k=6.0 \times 10^6 kg / h$ ).问从着陆点算起,飞机滑行的最长距离是多少?
差分方程 $2 y_{t+1}+10 y_t-5 t=0$ 的通解为