单选题 (共 3 题 ),每题只有一个选项正确
设 $C$ 为正向圆周 $|z|=\frac{1}{2}$ ,则 $\int_C \frac{z^2 \cos \frac{1}{z-2}}{(1-z)^2} d z$ 的值为( ).
$\text{A.}$ $2 \pi i (3 \cos 1-\sin 1)$
$\text{B.}$ 0
$\text{C.}$ $6 \pi i \cos 1$
$\text{D.}$ $-2 \pi \operatorname{isin} 1$
设 $f(z)$ 在单连通区域 $B$ 内处处解析且不为零,$C$ 为 $B$ 内任意一条简单闭曲线,则积分 $\int_C \frac{f^{\prime \prime}(z)+2 f^{\prime}(z)+f(z)}{f(z)} d z=(\quad)$ 。
$\text{A.}$ $2 \pi i$
$\text{B.}$ $-2 \pi i$
$\text{C.}$ 0
$\text{D.}$ 不确定
设路径 $C$ 为以 $(0,-1),(1,-1),(1,1),(0,1)$ 为顶点的四边形,则积分 $\int_{-i}^i \frac{d z}{z}$ 的值为( )。
$\text{A.}$ $\pi$
$\text{B.}$ $\pi i$
$\text{C.}$ $2 \pi$
$\text{D.}$ $2 \pi i$
填空题 (共 3 题 ),请把答案直接填写在答题纸上
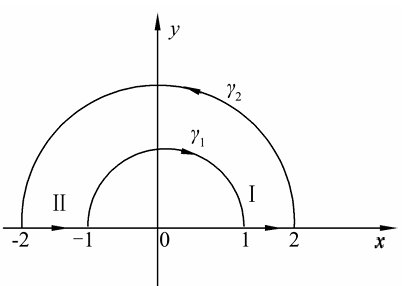
设 $\Gamma$ 是闭圆环 $1 \leqslant|z| \leqslant 2$ 上半部分的边界,其方向如图 3.2 所示.则复积分
$$
\int_{\Gamma} \frac{z}{\bar{z}} d z=
$$
设 $\Gamma$ 为连接点— i 到 i 的直线段.
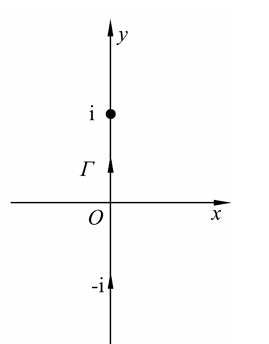
试证:$\left|\int_{\Gamma}\left(x^2+ i y^2\right) d z\right| \leqslant 2$ .
设 $C$ 为连接 0 到 $2 \pi a$ 的摆线:$x=a(\theta-\sin \theta), y=a(1-\cos \theta)$ ,则积分 $\int_C\left(2 z^2+8 z+1\right) d z$的值为
解答题 (共 4 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
沿如下路线 $C_j(j=1,2,3)$ 计算.
$\int_{C_j}\left(x^2+y^2\right) d x-2 x y d y$ 起点和终点都是 $(1,0)$ 和 $(0,1)$ .
$C_1: x+y=1$(一条直线段);
$C_2: x^2+y^2=1$(单位圆周上一段弧);
$C_3:\left\{\begin{array}{l}z(t)=1+ i t \quad(0 \leqslant t \leqslant 1) \\ z(t)=(2-t)+ i \quad(1 \leqslant t \leqslant 2)\end{array}\right.$(一条折线)。
(1)设 $\gamma$ 是上半单位圆周(取逆时针旋转),则
$$
\left|\int_\gamma \frac{e^z}{z} d z\right| \leqslant \pi e ;
$$
(2)又 $C$ 为单位圆周(逆时针方向),则
$$
\left|\int_C \frac{\sin z}{z^2} d z\right| \leqslant 2 \pi e .
$$
设 $C$ 为正向圆周 $|z|=a>0$ ,则积分 $\int_C\left(|z|-e^z \sin z\right) d z=$ $\qquad$ .
设 $C$ 为不穿过 $a$ 与 $-a$ 的正向简单闭曲线,$a$ 为不等于零的任意复数,计算积分 $\int_C \frac{z d z}{z^2-a^2}$.
证明题 (共 1 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设 $C$ 为圆周 $|z|=1$ ,计算 $\int_C \frac{d z}{z+1}$ ,并由此证明:
$$
\int_0^\pi \frac{1+2 \cos \theta}{5+4 \cos \theta} d \theta=0 .
$$