单选题 (共 2 题 ),每题只有一个选项正确
将矩形纸片 $A B C D$ 沿 $B D$ 折叠得到 $\triangle B C^{\prime} D, C^{\prime} D$ 与 $A B$ 交于点 $E$ ,若 $\angle 1=35^{\circ}$ ,则 $\angle 2$ 的度数为
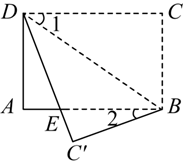
$\text{A.}$ $15^{\circ}$
$\text{B.}$ $20^{\circ}$
$\text{C.}$ $25^{\circ}$
$\text{D.}$ $30^{\circ}$
如图,把菱形 $A B C D$ 沿 $A H$ 折叠,使 $B$ 点落在 $B C$ 上的 $E$ 点处,若 $\angle B=70^{\circ}$ ,则 $\angle E D C$ 的大小为
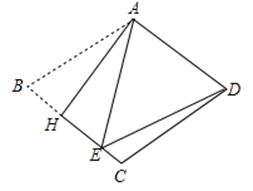
$\text{A.}$ $15^{\circ}$
$\text{B.}$ $20^{\circ}$
$\text{C.}$ $30^{\circ}$
$\text{D.}$ $25^{\circ}$
填空题 (共 1 题 ),请把答案直接填写在答题纸上
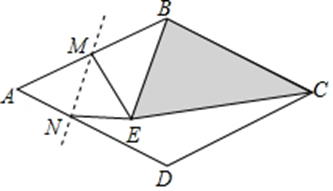
如图,菱形 $A B C D$ 的周长为 8 厘米,$\angle D=120^{\circ}$ ,点 $M$ 为 $A B$ 的中点,点 $N$ 是边 $A D$ 上任一点,把 $\angle A$ 沿直线 $M N$折叠,点 $A$ 落在图中的点 $E$ 处,当 $A N=$ $\qquad$厘米时,$\triangle B C E$ 是直角三角形.
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
如图,在菱形 $A B C D$ 中,$\angle A=120^{\circ}, A B=2$ ,点 $E$ 是边 $A B$ 上一点,以 $D E$ 为对称轴将 $\triangle D A E$ 折叠得到 $\triangle D G E$ ,再折叠 $B E$ 使 $B E$ 落在直线 $E G$ 上,点 $B$ 的对应点为点 $H$ ,折痕为 $E F$ 且交 $B C$ 于点 $F$ .
(1)$\angle D E F=$ $\qquad$ ;
(2)若点 $E$ 是 $A B$ 的中点,则 $D F$ 的长为 $\qquad$ .
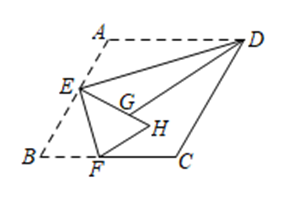
如图 1,在正方形 $A B C D$ 中,点 $E$ 为 $B C$ 上一点,连接 $D E$ ,把 $\triangle D E C$ 沿 $D E$ 折叠得到 $\triangle D E F$ ,延长 $E F$ 交 $A B$ 于 $G$ ,连接 $D G$ .
(1)求证:$\angle E D G=45^{\circ}$ .
(2)如图 2,$E$ 为 $B C$ 的中点,连接 $B F$ .
① 求证:$B F \| D E$ ; ② 若正方形边长为 6 ,求线段 $A G$ 的长.
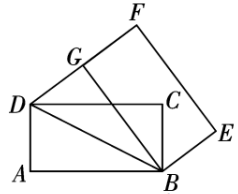
如图,四边形 $A B C D$ 是矩形,以点 $B$ 为旋转中心,顺时针旋转矩形 $A B C D$ 得到矩形 $G B E F$ ,点 $A, D, C$ 的对应点分别为点 $G, F, E$ ,点 $D$ 恰好在 $F G$ 的延长线上.
(1)求证:$\triangle B D A \cong \triangle B D G$ :
(2)若 $A D=2$ ,求 $D F$ 的长.
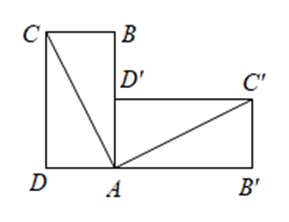
如图,将矩形 $A B C D$ 绕点 $A$ 顺时针旋转 $90^{\circ}$ 后,得到矩形 $A B^{\prime} C^{\prime} D^{\prime}$ ,如果 $C D=2 D A=2$ ,那么 $C C^{\prime}=$ $\qquad$ .
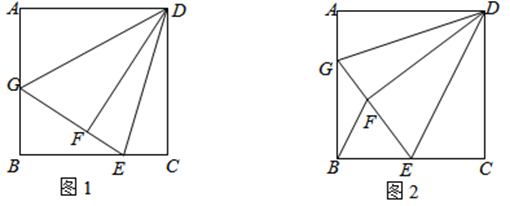
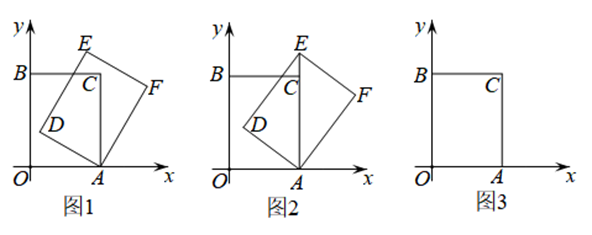
在平面直角坐标系中,四边形 $A O B C$ 是矩形,点 $O(0,0)$ ,点 $A(3,0)$ ,点 $B(0,4)$ .以点 $A$ 为中心,顺时针旋转矩形 $A O B C$ ,得到矩形 $A D E F$ ,点 $O, B, C$ 的对应点分别为 $D, E, F$ ,记旋转角为 $\alpha\left(0^{\circ} < \alpha < 90^{\circ}\right)$ .
(1)如图 1,当 $\alpha=30^{\circ}$ 时,求点 $D$ 的坐标;
(2)如图 2,当点 $E$ 落在 $A C$ 的延长线上时,求点 $D$ 的坐标;
(3)当点 $D$ 落在线段 $O C$ 上时,直接写出点 $E$ 的坐标.
综合与实践
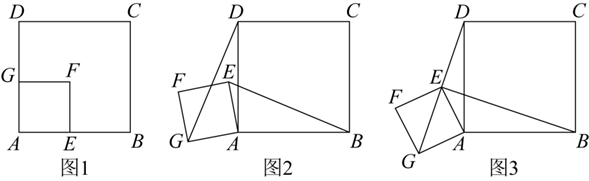
【情境呈现】如图 1,将两个正方形纸片 $A B C D$ 和 $A E F G$ 放置在一起.若固定正方形 $A B C D$ ,将正方形 $A E F G$ 绕着点 $A$ 旋转.
(1)【数学思考】如图 1 ,当点 $E$ 在 $A B$ 边上,点 $G$ 在 $A D$ 边上时,线段 $B E$ 与 $D G$ 的数量关系是 $\qquad$ ,位置关系是 $\qquad$ .
(2)如图 2,是将正方形 $A E F G$ 绕着点 $A$ 逆时针旋转 $\alpha$ 度得到的,则(1)中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
(3)【拓展探究】如图 3,若点 $D, E, G$ 在同一条直线上,且 $A B=2 A E=2 \sqrt{2}$ ,求线段 $B E$ 的长度(直接写出答案).