单选题 (共 9 题 ),每题只有一个选项正确
设全集 $U=\{1,2,3,4,5\}$ ,集合 $A=\{1,3\}, B=\{2,3,5\}$ ,则 $\complement_U(A \cup B)=$
$\text{A.}$ $\{1,2,3,4\}$
$\text{B.}$ $\{2,3,4\}$
$\text{C.}$ $\{2,4\}$
$\text{D.}$ $\{4\}$
已知 $x \in R$ ,则"$x=0$"是" $\sin 2 x=0$"的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分也不必要条件
已知函数 $y=f(x)$ 的图象如下,则 $f(x)$ 的解析式可能为
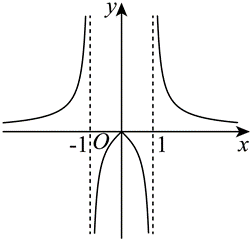
$\text{A.}$ $f(x)=\frac{x}{1-|x|}$
$\text{B.}$ $f(x)=\frac{x}{|x|-1}$
$\text{C.}$ $f(x)=\frac{|x|}{1-x^2}$
$\text{D.}$ $f(x)=\frac{|x|}{x^2-1}$
若 $m$ 为直线,$\alpha, \beta$ 为两个平面,则下列结论中正确的是( )
$\text{A.}$ 若 $m / / \alpha, n \subset \alpha$ ,则 $m / / n$
$\text{B.}$ 若 $m \perp \alpha, m \perp \beta$ ,则 $\alpha \perp \beta$
$\text{C.}$ 若 $m / / \alpha, m \perp \beta$ ,则 $\alpha \perp \beta$
$\text{D.}$ 若 $m \subset \alpha, \alpha \perp \beta$ ,则 $m \perp \beta$
下列说法中错误的是
$\text{A.}$ 若 $X \sim N\left(\mu, \sigma^2\right)$ ,则 $P(X \leq \mu-\sigma)=P(X \geq \mu+\sigma)$
$\text{B.}$ 若 $X \sim N\left(1,2^2\right), Y \sim N\left(2,2^2\right)$ ,则 $P(X < 1) < P(Y < 2)$
$\text{C.}$ $|r|$ 越接近 1 ,相关性越强
$\text{D.}$ $|r|$ 越接近 0 ,相关性越弱
$S_n=-n^2+8 n$ ,则数列 $\left\{\left|a_n\right|\right\}$ 的前 12 项和为( )
$\text{A.}$ 112
$\text{B.}$ 48
$\text{C.}$ 80
$\text{D.}$ 64
函数 $f(x)=0.3^x-\sqrt{x}$ 的零点所在区间是( )
$\text{A.}$ $(0,0.3)$
$\text{B.}$ $(0.3,0.5)$
$\text{C.}$ $(0.5,1)$
$\text{D.}$ $(1,2)$
$f(x)=\sin (\omega x+\varphi)(\omega>0,-\pi < \varphi < \pi)$ ,在 $\left[-\frac{5 \pi}{12}, \frac{\pi}{12}\right]$ 上单调递增,且 $x=\frac{\pi}{12}$ 为它的一条对称轴,$\left(\frac{\pi}{3}, 0\right)$ 是它的一个对称中心,当 $x \in\left[0, \frac{\pi}{2}\right]$ 时,$f(x)$ 的最小值为
$\text{A.}$ $-\frac{\sqrt{3}}{2}$
$\text{B.}$ $-\frac{1}{2}$
$\text{C.}$ -1
$\text{D.}$ 0
双曲线 $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的左、右焦点分别为 $F_1, F_2$ ,以右焦点 $F_2$ 为焦点的抛物线 $y^2=2 p x(p>0)$ 与双曲线交于第一象限的点 $P$ ,若 $\left|P F_1\right|+\left|P F_2\right|=3\left|F_1 F_2\right|$ ,则双曲线的离心率 $e=(\quad)$
$\text{A.}$ 2
$\text{B.}$ 5
$\text{C.}$ $\frac{\sqrt{2}+1}{2}$
$\text{D.}$ $\frac{\sqrt{5}+1}{2}$
填空题 (共 6 题 ),请把答案直接填写在答题纸上
已知 i 是虚数单位,则 $\left|\frac{3+ i }{i}\right|=$
在 $(x-1)^6$ 的展开式中,$x^3$ 项的系数为
$l_1: x-y+6=0$ ,与 $x$ 轴交于点 $A$ ,与 $y$ 轴交于点 $B$ ,与 $(x+1)^2+(y-3)^2=r^2$ 交于 C、 D 两点,$|A B|=3|C D|$ ,则 $r=$
小桐操场跑圈,一周 2 次,一次 5 圈或 6 圈.第一次跑 5 圈或 6 圈的概率均为 0.5 ,若第一次跑 5 圈,则第二次跑 5 圈的概率为 $0.4,6$ 圈的概率为 0.6 ;若第一次跑 6 圈,则第二次跑 5 圈的概率为 $0.6,6$ 圈的概率为 0.4 .小桐一周跑 11 圈的概率为 $\qquad$ ;若一周至少跑 11 圈为动量达标,则连续跑 4 周,记合格周数为 $X$ ,则期望 $E(x)=$
$\triangle A B C$ 中,$D$ 为 $A B$ 边中点, $\overrightarrow{C E}=\frac{1}{3} \overrightarrow{C D}, \overrightarrow{A B}=\vec{a}, \overrightarrow{A C}=\vec{b}$ ,则 $\overrightarrow{A E}=$ $\qquad$ (用 $\hat{a}, \hat{b}$ 表示),若 $|\overrightarrow{A E}|=5, A E \perp C B$ ,则 $\overrightarrow{A E} \cdot \overrightarrow{C D}=$
若 $a, b \in R$ ,对 $\forall x \in[-2,2]$ ,均有 $(2 a+b) x^2+b x-a-1 \leq 0$ 恒成立,则 $2 a+b$ 的最小值为
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在 $\triangle A B C$ 中,角 $A, B, C$ 的对边分别为 $a, b, c$ .已知 $a \sin B=\sqrt{3} b \cos A, c-2 b=1, a=\sqrt{7}$ .
(1)求 $A$ 的值;
(2)求 $c$ 的值;
(3)求 $\sin (A+2 B)$ 的值.
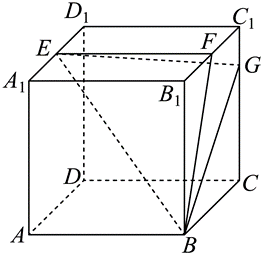
正方体 $A B C D-A_1 B_1 C_1 D_1$ 的棱长为 $4, E 、 F$ 分别为 $A_1 D_1, C_1 B_1$ 中点,$C G=3 G C_1$ .
(1)求证:$G F \perp$ 平面 $F B E$ ;
(2)求平面 $F B E$ 与平面 $E B G$ 夹角的余弦值;
(3)求三棱锥 $D-F B E$ 的体积.
已知椭圆 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的左焦点为 $F$ ,右顶点为 $A, P$ 为 $x=a$ 上一点,且直线 $P F$ 的斜率为 $\frac{1}{3}, \triangle P F A$ 的面积为 $\frac{3}{2}$ ,离心率为 $\frac{1}{2}$ .
(1)求椭圆的方程;
(2)过点 $P$ 的直线与椭圆有唯一交点 $B$(异于点 $A$ ),求证:$P F$ 平分 $\angle A F B$ .
已知数列 $\left\{a_n\right\}$ 是等差数列,$\left\{b_n\right\}$ 是等比数列,$a_1=b_1=2, a_2=b_2+1, a_3=b_3$ .
(1)求 $\left\{a_n\right\},\left\{b_n\right\}$ 的通项公式;
(2)$\forall n \in N^*, I \in\{0,1\}$ ,有 $T_n=\left\{p_1 a_1 b_1+p_2 a_2 b_2+\ldots+p_{n-1} a_{n-1} b_{n-1}+p_n a_n b_n \mid p_1, p_2, \ldots, p_{n-1}, p_n \in I\right\}$ ,
(i)求证:对任意实数 $t \in T_n$ ,均有 $t < a_{n+1} b_{n+1}$ ;
(ii)求 $T_n$ 所有元素之和.
已知函数 $f(x)=a x-(\ln x)^2$
(1)$a=1$ 时,求 $f(x)$ 在点 $(1, f(1))$ 处的切线方程;
(2)$f(x)$ 有 3 个零点,$x_1, x_2, x_3$ 且 $\left(x_1 < x_2 < x_3\right)$ .