行列式 $\left|\begin{array}{llll}0 & a & b & 0 \\ a & 0 & 0 & b \\ 0 & c & d & 0 \\ c & 0 & 0 & d\end{array}\right|=$

已知正实数 $a, b$, 满足条件 $2 a+b=1$, 则 $a b$ 的最大值为

日常生活中，人们经常面临需要排队的情形，某小组想要知道是否可以通过安排排队方式的方法让人们的排队时间更短:
实验研究：现有一个办事窗口，人们需要排队进行办公，每个人办事的时间称为他自身的办公时间，一个人除去自身办公以外所需消耗时间称为这个人的排队时间。如：若第一个人的办公时间为 3 ，第二个人的办公时间为 4 ，那么第一个人排队时间为 0 ，第二个人排队时间为 3 ，第三个人的排队时间为 7 。
不难发现，对每个人来说满足排队时间最短的方式是排在队伍的首位，这时排队时间为 0 ，但这对每个人来说不能同时满足. 于是小组希望研究出最合适的安排可以使所有人的总排队时间最短.
假设现有三人需要排队办公, 分别为甲、乙、丙, 他们的办公时间分别为 $20 、 23 、 29$.
数据计算：对三种排队方案进行计算比较。
方案一：排队方式顺次为甲、乙、丙，则排队时间为 ________ .
方案二：排队方式顺次为乙、丙、甲，则排队时间为 ________ 。
方案三：排队方式顺次为丙、乙、甲，则排队时间为 ________ 。
实验结论：对比可知，方案 ________ 的排队时间最短。（填"—"、"二"、"三"）
推广证明：甲、乙、丙三人排队办公, 他们的办公时间分别为 $a 、 b 、 c$ （其中 $a < b < c$ ），请给出所有的排队方式，从中选出排队时间最短的方案并证明.

如图 $1, A B$ 是半圆 $O$ 的直径, 点 $C, D$ 是半圆 $O$ 上的点, 且 $A C \| O D$, 连结 $B C$ 交 $O D$ 于点 $E$.
(1) 求证: $O D \perp B C$.
(2) 如图 2 , 连结 $C D, A D, B D$, 若 $\sin \angle A B C=\frac{1}{3}$, 求 $\triangle A C D$ 与 $\triangle O B D$ 的面积之比.
(3) 如图3, 连结 $B D$, 作 $C P \| B D$ 交 $A B$ 于点 $P$, 连结 $P D$. 求证: $B D^2=B O \cdot B P$.

如图, 在平面直角坐标系中, 抛物线 $y=-\frac{1}{2} x^2+b x+c$ 与 $x$ 轴分别交于点 $A(-2,0), B(4,0)$, 与 $y$ 轴交于点 $C$, 连接 $B C$.
(1) 求抛物线的解析式;
(2) 如图1, 点 $P$ 是第一象限内抛物线上的一个动点, 过点 $P$ 作直线 $l \perp x$ 轴于点 $M(m, 0)$, 交 $B C$ 于点 $N$, 连接 $C M, P B, P C . \triangle P C$ $B$ 的面积记为 $S_1, \triangle B C M$ 的面积记为 $S_2$, 当 $S_1=S_2$ 时, 求 $m$ 的值；
(3) 在 (2) 的条件下, 点 $Q$ 在抛物线上, 直线 $M Q$ 与直线 $B C$ 交于点 $H$, 当 $\triangle H M N$ 与 $\triangle B C M$ 相似时, 请直接写出点 $Q$ 的坐标.

如图, 在 $\triangle A B C$ 中, $A B=A C$, 以 $A B$ 为直径的 $\odot O$ 交边 $A C$ 于点 $D$ (点 $D$ 不与点 $A$ 重合), 交边 $B C$ 于点 $E$, 过点 $E$ 作 $E F \perp A C$, 垂足为 $F$.
(1) 求证: $E F$ 是 $\odot O$ 的切线;
(2) 连接 $D E$, 求证: $\triangle D E C$ 是等腰三角形;
(3) 若 $C D=2, B E=3$, 求 $\odot O$ 的半径.

某数学活动小组在一次活动中, 对一个数学问题做了如下研究:

【问题发现】
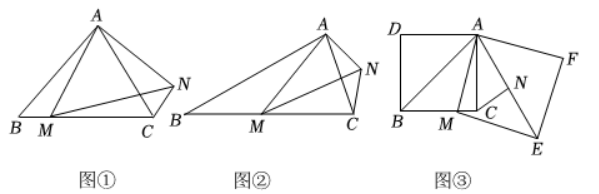
(1) 如图①, 在等边三角形 $A B C$ 中, 点 $M$ 是 $B C$ 边上任意一点, 连接 $A M$, 以 $A M$ 为边作等边三角形 $A M N$, 连接 $C N$, 则 $\angle A B C$ 和 $\angle A$ $C N$ 的数量关系为多少?
【变式探究】
(2) 如图②, 在等腰三角形 $A B C$ 中, $A B=B C$, 点 $M$ 是 $B C$ 边上任意一点 (不含端点 $B, C$ ), 连接 $A M$, 以 $A M$ 为边作等腰三角形 $A M$ $N$, 使 $\angle A M N=\angle A B C, A M=M N$, 连接 $C N$, 试探究 $\angle A B C$ 与 $\angle A C N$ 的数量关系, 并说明理由；
【解决问题】
(3) 如图③, 在正方形 $A D B C$ 中, 点 $M$ 为 $B C$ 边上一点, 以 $A M$ 为边作正方形 $A M E F$, 点 $N$ 为正方形 $A M E F$ 的中心, 连接 $C N, A B, A$ $E$, 若正方形 $A D B C$ 的边长为 $8, C N=\sqrt{2}$, 求正方形 $A M E F$ 的边长.

根据以下素材, 探索完成任务一:
如何设计购买方案?
素材1： 某校 40 名同学要去参观航天展览馆, 已知展览馆分为 A, B, C 三个场馆, 且购买1张 A 场馆门票和1 张B 场馆门票共需 90 元, 购买3 张 A 场馆门票和 2 张 B 场馆门票共需 230 元， C 场馆门票为每张 15 元

素材2：由于场地原因, 要求到 A 场馆参观的人数要少于到 B 场馆参观的人数, 且每位同学只能选择一个场馆参观. 参观当天刚好 有优惠活动: 每购买 1 张 场馆门票就赠送1 张 C 场馆门票.

任务1：确定场馆门票价格，求A,B场馆的门票价格
任务2：探究经费的使用
若购买A场馆门票赠送的C场馆门票刚好够参观C场馆的同学使用，求此次购买门票所需要的总金额的最小值
任务3 若参观 $C$ 场馆的同学除了使用掉赠送的门票外, 还需购买部分门票, 且让去 $A$ 场馆的人数尽量的多, 最终购买三种门票共花费了 1100 元, 请你直接写出购买方案.


探索完成任务二:
如图, 在参观航天展览馆活动中, 某班学生分成两组, 第一组由 $A$ 场馆匀速步行到 $B$ 场馆后原路原速返回, 第二组由 $A$ 场馆匀速步行到 $B$ 场馆继续前行到 $C$ 场馆后原路原速返回. 两组同时出发, 设步行的时间为 $t$ (单位: $h$ ), 两组离 $B$ 场馆的距离为 $s$ (单位: $k$ $m)$, 图中折线分别表示两组学生 $s$ 与 $t$ 之间的函数关系.


(1) $B, C$ 两场馆之间的距离为 ________ $k m$;
(2) 第二组步行的速度为 ________
（3）求第二组由 $A$ 场馆出发首次到达 $B$ 场馆所用的时间.

如图, 某渔船沿正东方向以 30 海里/小时的速度航行, 在 $A$ 处测得岛 $C$ 在东北方向, 20 分钟后渔船航行到 $B$ 处, 测得岛 $C$ 在北偏东 $30^{\circ}$ 方向, 已知该岛 $C$ 周围 25 海里内有暗礁.
(参考数据: $\sqrt{3} \approx 1.732, \sqrt{2} \approx 1.414, \sin 75^{\circ} \approx 0.966, \cos 75^{\circ} \approx 0.259$. )
（1）如果渔船继续向东航行, 有无触礁危险？请说明理由.
(2) 如果渔船在 $B$ 处改为向东偏南 $15^{\circ}$ 方向航行, 有无触礁危险? 说明理由.

如图, 已知 $\triangle A B C$.
(1) 用尺规利用 $S S S$ 作 $\triangle B A D$, 使得 $\triangle B A D \cong \triangle A B C$, 且 $\triangle B A D$ 和 $\triangle A B C$ 在直线 $A B$ 的同一侧 (不写作图过程, 保留作图痕迹)；
(2) 连接 $C D$, 求证: $\triangle A D C \cong \triangle B C D$ ；
(3) 设 $A C$ 与 $B D$ 交于点 $O$, 若 $\angle A B C=115^{\circ}, \angle A C B=30^{\circ}$, 求 $\angle A C D$ 的度数.