单选题 (共 8 题 ),每题只有一个选项正确
已知 $M=\left\{x \left\lvert\,-\frac{1}{2} \leqslant \sin x \leqslant \frac{1}{2}\right.\right\}, N=\left\{-\frac{\pi}{4},-\frac{\pi}{6}, 0, \frac{\pi}{3}\right\}$, 则 $M \cap N=$
$\text{A.}$ $\left\{-\frac{\pi}{6}, 0\right\}$
$\text{B.}$ $\left\{-\frac{\pi}{4}, 0\right\}$
$\text{C.}$ $\left\{-\frac{\pi}{6}, 0, \frac{\pi}{3}\right\}$
$\text{D.}$ $\left\{-\frac{\pi}{4},-\frac{\pi}{6}, 0\right\}$
某公司购人了 400 根钢管拟切割打磨为其他产品, 统计钢管口径后得以下频数分布表:则这批钢管口径的中位数为

$\text{A.}$ 14.00 cm
$\text{B.}$ 15.25 cm
$\text{C.}$ 16.25 cm
$\text{D.}$ 16.50 cm
已知直线 $l_1:-m^2 x+y-1=0$, 直线 $l_2:(2 m-3) x+y-3=0$, 则 $m=-3$ 是 $l_1 / / l_2$ 的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分又不必要条件
已知向量 $\boldsymbol{a}=(2,1), \boldsymbol{b}=(m-2, m)$, 若 $\boldsymbol{a} / / \boldsymbol{b}$, 则 $|\boldsymbol{a}+\boldsymbol{b}|=$
$\text{A.}$ 5
$\text{B.}$ 3
$\text{C.}$ $\sqrt{5}$
$\text{D.}$ $\sqrt{2}$
在平面直角坐标系中, 将圆 $C: x^2+y^2=1$ 上所有点的横坐标伸长到原来的 2 倍, 纵坐标缩短为原来的 $\frac{1}{3}$, 则得到的新曲线的曲线方程为
$\text{A.}$ $\frac{x^2}{9}+4 y^2=1$
$\text{B.}$ $9 x^2+\frac{y^2}{4}=1$
$\text{C.}$ $4 x^2+\frac{y^2}{9}=1$
$\text{D.}$ $\frac{x^2}{4}+9 y^2=1$
在 $\triangle A B C$ 中, 内角 $A, B, C$ 的对边分别为 $a, b, c$, 且 $2 b(\sin 2 A-\sin B \cos C)=c \sin 2 B$, 若点 $D$ 在 $B C$边上, 且 $A D$ 平分 $\angle B A C$, 则 $A D=$
$\text{A.}$ $\frac{b^2+c^2}{\sqrt{b c}}$
$\text{B.}$ $\frac{b c}{b+c}$
$\text{C.}$ $\frac{\sqrt{3} b c}{b+c}$
$\text{D.}$ $\frac{b^2 c^2}{b^2+c^2}$
在电子游戏中, 若甲, 乙, 丙通关的概率分别是 $\frac{2}{3}, \frac{4}{5}, \frac{3}{4}$, 且三人通关与否相互独立, 则在甲, 乙, 丙中恰有两人通关的条件下, 甲通关的概率为
$\text{A.}$ $\frac{2}{5}$
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ $\frac{6}{13}$
$\text{D.}$ $\frac{7}{13}$
当 $a \geqslant \mathrm{e}$ 时, 方程 $\mathrm{e}^x+x+\ln x=\ln a+\frac{a}{x}$ 在 $[1,+\infty)$ 上根的个数为
$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ 3
多选题 (共 3 题 ),每题有多个选项正确
若 $z$ 在复平面内对应的点为 $A, z+2 \bar{z}=3+\sqrt{3} i$, 则
$\text{A.}$ $z$ 的实部为 1
$\text{B.}$ $z$ 的虚部为 $-\sqrt{3}$
$\text{C.}$ $|z|=4$
$\text{D.}$ 直线 $O A$ 的倾斜角为 $\frac{5 \pi}{6}$
已知 $O$ 为坐标原点, 点 $F(1,0)$ 是抛物线 $C: y^2=2 p x(p>0)$ 的焦点, 过点 $F$ 的直线交 $C$于 $M, N$ 两点, $P$ 为 $C$ 上的动点 (与 $M, N$ 均不重合), 且点 $P$ 位于第一象限, 过点 $P$ 向 $y$ 轴作垂线, 垂足记为点 $Q$, 点 $A(2,5)$, 则
$\text{A.}$ $C: y^2=4 x$
$\text{B.}$ $\angle O P Q+\angle F O N < 180^{\circ}$
$\text{C.}$ $|P A|+|P Q|$ 的最小值为 $\sqrt{26}$
$\text{D.}$ $\triangle O M N$ 面积的最小值为 2
已知函数 $f(x)$ 的定义域为 $\mathbf{R}$, 则
$\text{A.}$ 若 $f(2)>f(1)$, 则 $f(x)$ 是 $\mathbf{R}$ 上的单调递增函数
$\text{B.}$ 若 $f\left(x^2\right)=-f\left(-x^2\right)$, 则 $f(x)$ 是奇函数
$\text{C.}$ 若 $f(1-x)=f(1+x)$, 且 $f(2-x)=f(2+x)$, 则 $f(x+2)=f(x)$
$\text{D.}$ 若 $|f(x)|=|f(-x)|$, 则 $f(x)$ 是奇函数或 $f(x)$ 是偶函数
填空题 (共 3 题 ),请把答案直接填写在答题纸上
若 $2 m+5 n=\frac{1}{2}$, 则 $\log _2\left(4^m \times 32^n\right)=$
函数 $f(x)=\cos (\omega x+\varphi)\left(\omega>0, \frac{\pi}{2} < \varphi < \frac{3 \pi}{2}\right)$, 若 $f(x)$ 的一个单调递增区间为 $\left[-\frac{2}{3}, \frac{4}{3}\right]$, 且 $f(0)=-\frac{1}{2}$, 则 $f(1)=$
已知圆台的上、下底半径分别为 $r$ 和 $R$ ,若圆台外接球的球心在圆台外,则圆台的高的取值范围是 $\qquad$ ;若 $R=2 r=2$ ,圆台的高为 $h$ ,且 $1 \leqslant h \leqslant \sqrt{2}$ ,则圆台外接球表面积的最大值为
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在 $\triangle A B C$ 中, 已知内角 $A, B, C$ 所对的边分别为 $a, b, c$, 且 $a, b, c$ 依次为等比数列 $\left\{a_n\right\}$ 的前 3 项, 设其公比为 $q$, 且 $a>1, q \geqslant 1$.
(1) 若 $a=2, q \in\left\{\frac{3}{2}, 2\right\}$, 求 $\left\{a_n\right\}$ 的前 $n$ 项和 $S_n$;
(2)证明: 当 $\frac{a}{q}=\sqrt{2}$ 时, 长度为 $\lg a, \lg b, \lg c$ 的三条线段可以构成三角形.
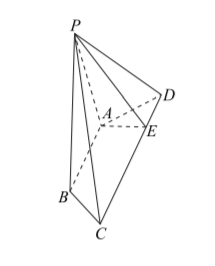
如图, 在四棱锥 $P-A B C D$ 中, $P A \perp$ 平面 $A B C D, A B / / C D, C D=2 A B=2 \sqrt{2}, P A=$ $B C=A D=1$.
(1) 求证:平面 $P B C \perp$ 平面 $P A D$;
(2) 若 $\overrightarrow{E C}=3 \overrightarrow{D E}$, 求平面 $P A E$ 与平面 $P B C$ 的夹角.
已知函数 $f(x)=\frac{1}{3} x^3+\frac{a}{2} x^2+2 x+b \sin x(a, b \in \mathbf{R})$.
(1) 当 $b=0$ 时, 若 $f(x)$ 存在极大值, 且存在极小值, 求 $a$ 的取值范围;
(2) 证明: 当 $a=2 b=2$ 时, $\forall x \in \mathbf{R}, f^{\prime}(x)>0$ 。
已知双曲线 $\Gamma: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的离心率为 $\frac{\sqrt{6}}{2}$, 焦距为 $2 \sqrt{3}$.
(1) 求 $\Gamma$ 的标准方程;
(2) 若过点 $(0,-b)$ 作直线 $l$ 分别交 $\Gamma$ 的左、右两支于 $A, B$ 两点, 交 $\Gamma$ 的渐近线于 $C$, $D$ 两点,求 $\frac{A B}{C D}$ 的取值范围.
将 4 个面上分别写有数字 $1,2,3,4$ 的一个正四面体在桌面上连续独立地抛 $n$ 次 $(n$ 为正整数), 设 $X$ 为与桌面接触的数字为偶数的次数, $p$ 为抛正四面体一次与桌面接触的数字为偶数的概率.
(1) 当 $n=5$ 时, 若正四面体的质地是均匀的, 求 $X$ 的数学期望和方差;
(2)若正四面体有瑕疵 ,即 $p \neq \frac{1}{2}$.
① 设 $p_n$ 是抛掷正四面体 $n$ 次中与桌面接触的数字为偶数出现奇数次的概率, 求证: $\phi_n=p+(1-2 p) p_{n-1}(n \geqslant 2)$ ;
② 求抛掷正四面体 $n$ 次中与桌面接触的数字为偶数出现偶数次的概率.