单选题 (共 34 题 ),每题只有一个选项正确
$\lim _{x \rightarrow 0} \frac{x^2-\sin ^2 x}{x^4}=$
$\text{A.}$ $-\frac{1}{3}$.
$\text{B.}$ $\frac{1}{3}$.
$\text{C.}$ $-\frac{1}{6}$.
$\text{D.}$ $\frac{1}{6}$.
$\text{E.}$ $1$
$\lim _{x \rightarrow 0}\left(2-2^x\right)^{\frac{1}{x}}=$
$\text{A.}$ 1.
$\text{B.}$ 2 .
$\text{C.}$ $\frac{1}{2}$.
$\text{D.}$ $\ln 2$.
$\text{E.}$ $\sqrt{e}$.
如图 1, 三条曲线是某个函数若 $f(x)$ 及其一阶导函数 $f^{\prime}(x)$ 与二阶导函数 $f^{\prime \prime}(x)$ 的图形, 则 $y=f(x), y=f^{\prime}(x), y=f^{\prime \prime}(x)$ 的图形依次是
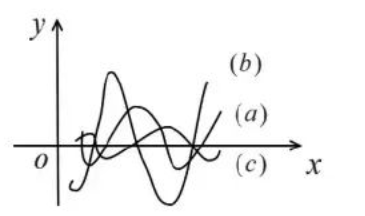
$\text{A.}$ $(a)(b)(c)$.
$\text{B.}$ $(b)(c)(a)$.
$\text{C.}$ $(c)(a)(b)$.
$\text{D.}$ $(b)(a)(c)$.
$\text{E.}$ $(c)(a)(b)$.
设 $b, k$ 为常数, 则函数 $f(x)=\left\{\begin{array}{l}k x+b, x < 1 \\ \sqrt{1+x^2}, x \geq 1\end{array}\right.$, 可导的充分必要条件是
$\text{A.}$ $k=0, b=\sqrt{2}$.
$\text{B.}$ $k=\frac{\sqrt{2}}{2}, b=\frac{\sqrt{2}}{2}$.
$\text{C.}$ $k=\sqrt{2}, b=0$.
$\text{D.}$ $k=\frac{2 \sqrt{2}}{3}, b=\frac{\sqrt{2}}{3}$.
$\text{E.}$ $k+b=\sqrt{2}$.
设实数数列 $\left\{a_n\right\}$, 给出以下四个命题:
1) 若 $\lim _{n \rightarrow \infty} a_n=A$, 则 $\lim _{n \rightarrow \infty} \sin a_n=\sin A$.
2) 若 $\lim _{n \rightarrow \infty} \sin a_n=\sin A$, 则 $\lim _{n \rightarrow \infty} a_n=A$.
3) 若 $\lim _{n \rightarrow \infty} a_n=A$, 则 $\lim _{n \rightarrow \infty} e^{a_n}=e^A$.
4) 若 $\lim _{n \rightarrow \infty} e^{a_n}=e^A$, 则 $\lim _{n \rightarrow \infty} a_n=A$.
其中真命题的个数是
$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ 3
$\text{E.}$ 4
设函数 $f(x)$ 在闭区间 $[a, b]$ 上有定义, 在开区间 $(a, b)$ 内可导, 则
$\text{A.}$ 当 $f(a) f(b) < 0$ 时, 存在 $\xi \in(a, b)$, 使得 $f(\xi)=0$.
$\text{B.}$ 当 $f(a)=f(b)$ 时, 存在 $\xi \in(a, b)$, 使得 $f^{\prime}(\xi)=0$.
$\text{C.}$ 当 $\lim _{x \rightarrow a^{+}} f(x)=\lim _{x \rightarrow b^{-}} f(x)$ 时, 存在 $\xi \in(a, b)$, 使得 $f^{\prime}(\xi)=0$.
$\text{D.}$ 当 $\lim _{x \rightarrow a^{+}} f(x)=f(a), \lim _{x \rightarrow b^{-}} f(x)=f(b)$ 时, 存在 $\xi \in(a, b)$, 使得 $f(\xi)=0$.
$\text{E.}$ 当 $\lim _{x \rightarrow a^{+}} f(x)=f(a), \lim _{x \rightarrow b^{-}} f(x)=f(b)$ 时, 存在 $\xi \in(a, b)$, 使得 $f^{\prime}(\xi)=0$.
设 $a$ 为正实数, 令 $I_a=\int_{\frac{1}{a}}^a \frac{\ln x}{1+x^2} d x$, 则
$\text{A.}$ $I_a=0$.
$\text{B.}$ $I_a=1$.
$\text{C.}$ $I_a=-1$.
$\text{D.}$ $I_a=2$.
$\text{E.}$ $I_a$ 的值与 $a$ 有关.
已知函数 $f(x)=\int_0^x x\left(e^{t^2}-1\right) d t$, 则
$\text{A.}$ $x=0$ 是 $f(x)$ 的极大值点, $(0,0)$ 是 $y=f(x)$ 的拐点.
$\text{B.}$ $x=0$ 是 $f(x)$ 的极小值点, $(0,0)$ 是 $y=f(x)$ 的拐点.
$\text{C.}$ $x=0$ 是 $f(x)$ 的极大值点, $(0,0)$ 不是 $y=f(x)$ 的拐点.
$\text{D.}$ $x=0$ 是 $f(x)$ 的极小值点, $(0,0)$ 不是 $y=f(x)$ 的拐点.
$\text{E.}$ $x=0$ 不是 $f(x)$ 的极值点, $(0,0)$ 不是 $y=f(x)$ 的拐点.
设函数 $f(x), g(x)$ 可导, 且 $f^{\prime}(1)=1, f^{\prime}(2)=2, g(1)=a, g^{\prime}(1)=4$, 令 $b=\left.\frac{d f(g(x))}{d x}\right|_{x=1}$, 则
$\text{A.}$ 当 $a=1$ 时,$b=4$.
$\text{B.}$ 当 $a=1$ 时,$b=5$.
$\text{C.}$ 当 $a=1$ 时,$b=8$.
$\text{D.}$ 当 $a=2$ 时,$b=6$.
$\text{E.}$ 当 $a=2$ 时, $b=7$.
已知平面区域 $D=\left\{(x, y) \mid 0 \leq y \leq 1-x^2,-1 \leq x \leq 1\right\}$, 则该区域绕 $x$轴旋转一周而成的旋转体的体积为
$\text{A.}$ $\frac{8}{15} \pi$.
$\text{B.}$ $\frac{16}{15} \pi$.
$\text{C.}$ $\frac{32}{15} \pi$.
$\text{D.}$ $\frac{38}{15} \pi$.
$\text{E.}$ $\frac{64}{15} \pi$.
设函数 $f(x)$ 二阶导数大于零且 $f(0)=f(2)=0$, 给出以下四个结论:
(1) 当 $x \in(0,2)$ 时, $f(x) < 0$.
(2) 当 $x \in(0,2)$ 时, $2 f(x)>\int_0^2 f(t) d t$.
(3)当 $x \neq 0$ 时, $f(x)>f^{\prime}(0) x$.
(4) 当 $x \neq 2$ 时, $f(x) < f^{\prime}(2)(x-2)$.
其中正确的是
$\text{A.}$ (1)(2).
$\text{B.}$ (1)(3).
$\text{C.}$ (1)(4).
$\text{D.}$ (2)(3).
$\text{E.}$ (2)(4).
已知反常积分 (1) $\int_{-\infty}^{+\infty} \frac{\sqrt[3]{x}}{1+x^4} d x$,
(2) $\int_{-\infty}^{+\infty} \frac{x}{1+x^4} d x$,
(3) $\int_{-\infty}^{+\infty} \frac{x \sqrt[3]{x}}{1+x^4} d x$, $\int_{-\infty}^{+\infty} \frac{x^3}{1+x^4} d x$, 其中收敛且值等于 0 的是
$\text{A.}$ (1)(2).
$\text{B.}$ (1)(3).
$\text{C.}$ (2)(4).
$\text{D.}$ (1)(2)(3).
$\text{E.}$ (1)(2)(4).
设函数 $e^x f(x)$ 的一个原函数是 $x^2$, 则 $\int_0^1 f(x) d x=$
$\text{A.}$ $e$
$\text{B.}$ -1 .
$\text{C.}$ $\frac{1}{e}$.
$\text{D.}$ $1-\frac{1}{e}$.
$\text{E.}$ $2-\frac{2}{e}$.
求函数 $\int_0^1 \frac{1}{\sqrt{x(1-x)}} d x$
$\text{A.}$ $\frac{\pi}{8}$.
$\text{B.}$ $\frac{\pi}{4}$.
$\text{C.}$ $\frac{\pi}{2}$.
$\text{D.}$ $\pi$.
$\text{E.}$ $2 \pi$.
设 D 是抛物线 $y=x^2$ 与其过点 $(0,-a)(a>0)$ 的两条切线围成的有界区域, 若 D 的面积等于 18 , 则 $a=$
$\text{A.}$ 12 .
$\text{B.}$ 9 .
$\text{C.}$ 8.
$\text{D.}$ 6 .
$\text{E.}$ 3
已知曲线 L 的参数方程 $\left\{\begin{array}{l}x=2 \cos ^3 t, \\ y=2 \sin ^3 t\end{array}\left(0 \leq t \leq \frac{\pi}{2}\right)\right.$, 则 L 的长度为
$\text{A.}$ 2 .
$\text{B.}$ 3.
$\text{C.}$ 5.
$\text{D.}$ 6 .
$\text{E.}$ 9
已知函数 $f(u)$ 可导且 $f^{\prime}(0)=2$, 设 $z=f\left(\arctan \frac{x}{y}\right)$, 则 $z=\left.\frac{\partial z}{\partial x}\right|_{(0,2)}$ 与 $z=\left.\frac{\partial z}{\partial y}\right|_{(0,2)}$ 的值依次为
$\text{A.}$ $\frac{1}{2}, \frac{1}{2}$.
$\text{B.}$ $\frac{1}{2},-\frac{1}{2}$.
$\text{C.}$ 1,0.
$\text{D.}$ 2,0 .
$\text{E.}$ $1,-1$.
已知 $D=\left\{(x, y) \mid x^2+y^2 \leq 16\right\}, f(x, y)=x^2-y^2+\frac{1}{3} y^3$, 则 $f(x, y)$ 在 D 上的
$\text{A.}$ 最大值为 16 , 最小值为 0 .
$\text{B.}$ 最大值为 16 , 最小值为 $-\frac{4}{3}$.
$\text{C.}$ 最大值为 16 , 最小值为 $-\frac{112}{3}$.
$\text{D.}$ 最大值为 18 , 最小值为 $-\frac{112}{3}$.
$\text{E.}$ 最大值为 18 , 最小值为 -38 .
设可微函数 $z=z(x, y)$ 由 $\sin \left(x+y^2\right)+\left(1+x^2+y\right) e^z=1$ 确定,则 $\left.\frac{\partial z}{\partial x}\right|_{(0,0)}$ 与 $\left.\frac{\partial z}{\partial y}\right|_{(0,0)}$ 的值依次为
$\text{A.}$ 1, 1.
$\text{B.}$ $1,-1$.
$\text{C.}$ $-1,1$.
$\text{D.}$ $-1,-1$.
$\text{E.}$ 0,0
已知函数 $f(x, y)=\frac{x^2+y^2}{x^2+y^2-x y}$, 则 $x \frac{\partial f(x, y)}{\partial x}+y \frac{\partial f(x, y)}{\partial y}=$
$\text{A.}$ 0.
$\text{B.}$ 1 .
$\text{C.}$ 2.
$\text{D.}$ 3 .
$\text{E.}$ 4
已知函数 $f(x, y)=x^2 y+2 x y+\frac{1}{3} y^2$, 则
$\text{A.}$ $(0,0)$ 是 $f(x, y)$ 的极值点.
$\text{B.}$ $(1,-1)$ 是 $f(x, y)$ 的极值点.
$\text{C.}$ $(-2,0)$ 是 $f(x, y)$ 的极值点.
$\text{D.}$ $(-1,1)$ 是 $f(x, y)$ 的最大极值点.
$\text{E.}$ 由 $f(x, y)=x^2 y+2 x y+\frac{1}{3} y^3$
已知 $\left|\begin{array}{cccc}x & -m & -1 & 0 \\ 0 & -x & m & 1 \\ -1 & 0 & x & -m \\ m & 1 & 0 & -x\end{array}\right|=a_4 x^4+a_3 x^3+a_2 x^2+a_1 x^1+a_0$,则 $a_4+a_3+a_2+a_1+a_0=$
$\text{A.}$ $-m^4+4 m^2$.
$\text{B.}$ $m^4+4 m^2$.
$\text{C.}$ $-m^4+2 m^2$.
$\text{D.}$ $-4 m^4-4 m^2$.
设 $A, B$ 是三阶可逆矩阵, $A^*$ 是 $A$ 的伴随矩阵, 若 $|A|=2$, 则
$$
\left(A^* B^{-1} A\right)^{-1}=
$$
$\text{A.}$ $\frac{1}{2} A^{-1} B A$.
$\text{B.}$ $\frac{1}{8} A^{-1} B A$.
$\text{C.}$ $2 A^{-1} B A$.
$\text{D.}$ $\frac{1}{2} A B A^{-1}$.
已知向量组 $\alpha_1, \alpha_2, \alpha_3$ 线性无关, 则以下向量组中线性相关的是
$\text{A.}$ $\alpha_1+\alpha_2, \alpha_2+\alpha_3, 2 \alpha_1+\alpha_2+\alpha_3$.
$\text{B.}$ $\alpha_1+2 \alpha_2, \alpha_2+2 \alpha_3, \alpha_3+2 \alpha_1$.
$\text{C.}$ $\alpha_1+\alpha_2, \alpha_2+\alpha_3, \alpha_1+\alpha_2+2 \alpha_3$.
$\text{D.}$ $\alpha_1+\alpha_2, \alpha_2+\alpha_3, \alpha_1+2 \alpha_2+\alpha_3$.
设 $A$ 为 2 阶可逆矩阵, $A^{-1}=\left(\begin{array}{ll}a_{11} & a_{12} \\ a_{21} & a_{22}\end{array}\right)$. 将 $A$ 第一行的 2 倍加到第二行上, 得到矩阵 $B$, 则 $B^{-1}=$
$\text{A.}$ $\left(\begin{array}{ll}a_{11}-\frac{1}{2} a_{12} & a_{12} \\ a_{21}-\frac{1}{2} a_{22} & a_{22}\end{array}\right)$.
$\text{B.}$ $\left(\begin{array}{ll}a_{11} & a_{12}+\frac{1}{2} a_{11} \\ a_{21} & a_{22}+\frac{1}{2} a_{21}\end{array}\right)$.
$\text{C.}$ $\left(\begin{array}{ll}a_{11}-2 a_{12} & a_{12} \\ a_{21}-2 a_{22} & a_{22}\end{array}\right)$.
$\text{D.}$ $\left(\begin{array}{ll}a_{11}+2 a_{12} & a_{12} \\ a_{21}+2 a_{22} & a_{22}\end{array}\right)$.
已知向量
$$
\alpha_1=(1,-3,4), \alpha_2=(1,-2,2), \alpha_3=(1,-2,4), \alpha_4=(1,0,-2), \alpha_5=(0,1,1)
$$
则以下向量组中线性相关的是
$\text{A.}$ $\alpha_1, \alpha_2, \alpha_3$.
$\text{B.}$ $\alpha_2, \alpha_3, \alpha_4$.
$\text{C.}$ $\alpha_3, \alpha_4, \alpha_5$.
$\text{D.}$ $\alpha_1, \alpha_2, \alpha_4$.
设方程组 $\left\{\begin{array}{l}x_2+x_3-x_4=10 \\ x_1+3 x_3+x_4=13 \\ x_1+4 x_2+x_3=23\end{array}\right.$, 线性无关的解向量组中的向量个数最多为 $s$, 其对应的齐次线性方程组基础解系中的向量个数为 $t$, 则
$\text{A.}$ $s=1, t=1$.
$\text{B.}$ $s=2, t=1$.
$\text{C.}$ $s=2, t=3$.
$\text{D.}$ $s=3, t=2$.
AB 为随机事件, $\vec{B}$ 为对立事件, $P(A)=\frac{1}{3}, P(A \mid B)=\frac{1}{2}$, $P(A \mid B)=\frac{1}{5}$, 则 $P(B \mid A)=$
$\text{A.}$ $\frac{2}{9}$.
$\text{B.}$ $\frac{1}{3}$.
$\text{C.}$ $\frac{4}{9}$.
$\text{D.}$ $\frac{2}{3}$.
设 $A 、 B 、 C$ 为随机事件, $P(A)=P(B)=P(C)=\frac{1}{4}$, $P(A B)=P(B C)=P(A C)=\frac{1}{6}, P(A \cup B \cup C)=\frac{3}{8}$, 则 $P(C \mid A B)=$
$\text{A.}$ $\frac{1}{16}$.
$\text{B.}$ $\frac{1}{4}$.
$\text{C.}$ $\frac{1}{2}$.
$\text{D.}$ $\frac{2}{3}$.
设随机变量 $X$ 的概率密度函数与分布函数分别是 $f(x)$ 和 $F(x)$, 若 $f(x)=f(-x)$, 则 $F(-1)=(\quad)$
$\text{A.}$ $F(1)$
$\text{B.}$ $1-\int_0^1 f(x) d x$
$\text{C.}$ $\frac{1}{2}-\int_0^1 f(x) d x$
$\text{D.}$ $\frac{1}{4}-\int_0^1 f(x) d x$
设随机变量 $X$ 服从参数为 $\lambda$ 的泊松分布, 且 $E\left(X^2\right)-5 E X+4=0$, 则 $\lambda=(\quad)$
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
设随机变量 $X$ 服从区间 $[0,2]$ 上的均匀分布, 若 $P\left(X^2 \leq a\right)=\frac{1}{4}$, 则 $a=$
$\text{A.}$ $\frac{1}{4}$.
$\text{B.}$ $\frac{1}{2}$.
$\text{C.}$ $\frac{\sqrt{2}}{2}$.
$\text{D.}$ 1.
已知随机变量 X 的分布律为 $P(X=k)=\frac{1}{6}(k=1,2, \cdots, 6)$. 设 $f(x)=x^2+a x+12$, 若 $E(f(X))=\frac{8}{3}$, 则 $a=$
$\text{A.}$ -4 .
$\text{B.}$ -5 .
$\text{C.}$ -6 .
$\text{D.}$ -7 .
设随机变量 $X \sim N\left(2,3^2\right)$, 则 $D(2 X+3)=$
$\text{A.}$ 9.
$\text{B.}$ 18.
$\text{C.}$ 21 .
$\text{D.}$ 36.