单选题 (共 8 题 ),每题只有一个选项正确
设集合 $A=\{x \mid \ln (x-1) \leqslant 0\}, B=\{x \mid 0 \leqslant 2 x-1 \leqslant 2\}$, 则 $A \cup B=$
$\text{A.}$ $\left\{x \left\lvert\, 1 < x \leqslant \frac{3}{2}\right.\right\}$
$\text{B.}$ $\{x \mid x \leqslant 2\}$
$\text{C.}$ $\left\{x \left\lvert\, \frac{1}{2} \leqslant x \leqslant 2\right.\right\}$
$\text{D.}$ $\left\{x \left\lvert\, \frac{1}{2} \leqslant x \leqslant \frac{3}{2}\right.\right\}$
已知复数 $z$ 满足 $(1- i ) z=4+ i$, 则 $z$ 的共轭复数在复平面内对应的点位于
$\text{A.}$ 第一象限
$\text{B.}$ 第二象限
$\text{C.}$ 第三象限
$\text{D.}$ 第四象限
已知变量 $x$ 和变量 $y$ 的一组成对样本数据为 $\left(x_i, y_i\right)(i=1,2,3, \cdots, 8)$, 其中 $\bar{x}=\frac{9}{8}$, 其回归直线方程为 $\hat{y}=2 x-\frac{1}{4}$, 当增加两个样本数据 $(-1,5)$ 和 $(2,9)$ 后, 重新得到的回归直线方程斜率为 3 , 则在新的回归直线方程的估计下, 样本数据 $(4,10)$ 所对应的残差为
$\text{A.}$ -2
$\text{B.}$ -1
$\text{C.}$ 1
$\text{D.}$ -3
若正整数 $a, b$ 满足等式 $2023^{2025}=2024 a+b$, 且 $b < 2024$, 则 $b=$
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 2022
$\text{D.}$ 2023
已知 $a, b$ 均为非零向量, 其夹角为 $\theta$, 则 " $\cos \theta=1$ "是 " $|a-b|=|a|-|b|$ "的
$\text{A.}$ 充要条件
$\text{B.}$ 充分不必要条件
$\text{C.}$ 必要不充分条件
$\text{D.}$ 既不充分也不必要条件
已知等比数列 $\left\{a_n\right\}$ 满足 $\frac{1}{a_1}+\frac{1}{a_2}+\frac{1}{a_3}=14, a_2=\frac{1}{4}$, 记 $S_n$ 为其前 $n$ 项和, 则 $S_3=$
$\text{A.}$ $\frac{7}{8}$
$\text{B.}$ $\frac{7}{4}$
$\text{C.}$ $\frac{7}{2}$
$\text{D.}$ 7
已知直线 $l$ 经过抛物线 $C: y^2=4 x$ 的焦点, 且与抛物线交于 $A, B$ 两点, 若使得 $\overrightarrow{O P}=\overrightarrow{O A}$ $+\overrightarrow{O B}$ 成立的点 $P$ 的横坐标为 3 , 则四边形 $O A P B$ 的面积为
$\text{A.}$ $2 \sqrt{5}$
$\text{B.}$ $3 \sqrt{5}$
$\text{C.}$ $4 \sqrt{5}$
$\text{D.}$ $5 \sqrt{5}$
如图, 在三棱锥 $P-A B C$ 中, $P A=P B=C A=C B=2, \angle A P B=$ $\angle A C B=\frac{\pi}{2}, E, F, G$ 分别为 $P A, P B, P C$ 上靠近点 $P$ 的三等分点, 若此时恰好存在一个小球与三棱锥 $P-A B C$ 的四个面均相切, 且小球同时还与平面 $E F G$ 相切, 则 $P C=$
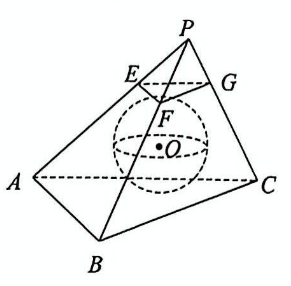
$\text{A.}$ $\sqrt{6}+\sqrt{2}$
$\text{B.}$ $\sqrt{6}-\sqrt{2}$
$\text{C.}$ $\sqrt{13}+1$
$\text{D.}$ $\sqrt{13}-1$
多选题 (共 3 题 ),每题有多个选项正确
下列结论正确的是
$\text{A.}$ 若 $x>0$, 则 $\frac{2 x}{x^2+1} \leqslant 1$
$\text{B.}$ 若 $x>y>0, z>0$, 则 $\frac{y}{x}>\frac{y+z}{x+z}$
$\text{C.}$ 若 $x y \neq 0$ 且 $x < y$, 则 $\frac{1}{x}>\frac{1}{y}$
$\text{D.}$ 若 $x>y>0$, 则 $x+\frac{1}{y}>y+\frac{1}{x}$
已知函数 $f(x)=A \sin (\omega x+\varphi)(A>0,0 < \varphi < 2 \pi)$ 的部分图象如图所示, 则
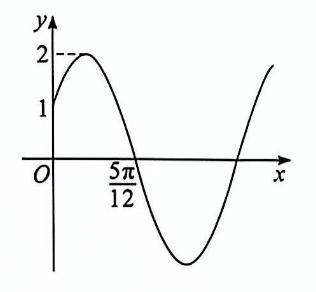
$\text{A.}$ $f(x)$ 在区间 $\left[-\frac{\pi}{3}, \frac{\pi}{6}\right]$ 上单调递增
$\text{B.}$ $f(x)$ 图象的一条对称轴方程为 $x=\frac{2 \pi}{3}$
$\text{C.}$ $f(x)$ 图象的一个对称中心为点 $\left(\frac{11 \pi}{12}, 0\right)$
$\text{D.}$ $f(x)$ 在区间 $\left[0, \frac{\pi}{4}\right]$ 上的值域为 $[1, \sqrt{3}]$
甲同学想用一支铅笔从如下的直三棱柱的顶点 $C_1$ 出发沿三棱柱的棱逐步完成"一笔画", 即每一步均沿着某一条棱从一个端点到达另一个端点, 紧接着从上一步的终点出发随机选择下一条棱再次画出,进而达到该棱的另一端点,按此规律一直进行,其中每经过一条棱称为一次移动,并随机选择某个顶点处停止得到一条"一笔画"路径,比如 "一笔画"路径 $C_1 \rightarrow B_1 \rightarrow A_1 \rightarrow A \rightarrow C$ 。若某"一笔画"路径中没有重复经过任何一条棱,则称该路径为完美路径,否则为不完美路径.下列说法正确的有
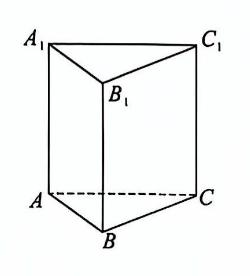
$\text{A.}$ 若"一笔画"路径为完美路径,则甲不可能 6 次移动后回到点 $C_1$
$\text{B.}$ 经过 4 次移动后仍在点 $C_1$ 的概率为 $\frac{19}{81}$
$\text{C.}$ 若"一笔画"路径为完美路径,则 5 次移动后回到点 $C_1$ 有 5 条不同笔迹
$\text{D.}$ 经过 3 次移动后, 到达点 $A_1$ 的条件下经过点 $C$ 的概率为 $\frac{1}{3}$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
设 $F$ 为双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的左焦点, $\alpha, \beta$ 分别为双曲线 $C$ 的两条渐近线的倾斜角, 已知点 $F$ 到其中一条渐近线的距离为 2 , 且满足 $\alpha=\frac{1}{5} \beta$, 则双曲线 $C$ 的焦距为
某流水线上生产的一批零件, 其规格指标 $X$ 可以看作一个随机变量, 且 $X \sim N\left(98, \sigma^2\right)$,对于 $X \geqslant 100$ 的零件即为不合格,不合格零件出现的概率为 0.05 ,现从这批零件中随机抽取 500 个,用 $Y$ 表示这 500 个零件的规格指标 $X$ 位于区间 $(96,100)$ 的个数,则随机变量 $Y$ 的方差是
已知函数 $f(x)=a^{x-1}-\log _a(x-1)$ (其中 $a>0$, 且 $a \neq 1$ ) 为其定义域上的单调函数, 则实数 $a$ 的取值范围为
在 $\triangle A B C$ 中, 内角 $A, B, C$ 所对的边分别为 $a, b, c$, 且 $\frac{1+\sin A}{\cos A}=\frac{1+\sin B}{\cos B}$.
(1)判断 $\triangle A B C$ 的形状;
(2)设 $A B=2$, 且 $D$ 是边 $B C$ 的中点, 求当 $\angle C A D$ 最大时 $\triangle A B C$ 的面积.