单选题 (共 10 题 ),每题只有一个选项正确
已知 $\alpha(x)=\left(\frac{x^3+x^4}{x^2+x^4+1}\right)^{\frac{1}{3}}-\ln (1+x), \beta(x)=x^3 \ln |x|, \gamma(x)=\ln \left(x+\sqrt{1+x^2}\right)-x$ ,当 $x \rightarrow 0$ 时,按无穷小阶数由高到低的顺序排列为( )。
$\text{A.}$ $\alpha(x), \beta(x), \gamma(x)$
$\text{B.}$ $\beta(x), \gamma(x), \alpha(x)$
$\text{C.}$ $\gamma(x), \beta(x), \alpha(x)$
$\text{D.}$ $\gamma(x), \alpha(x), \beta(x)$
已知 $f(x)$ 在 $x=0$ 的某邻域内有定义,在 $x=0$ 的某去心邻域内可导,且极限 $\lim _{x \rightarrow 0} f^{\prime}(x)$ 存在,下列说法正确的为( )。
$\text{A.}$ 若极限 $\lim _{x \rightarrow 0} \frac{f^{\prime}(x)+f(x)}{x}$ 存在,则 $f(x)$ 在 $x=0$ 处可导
$\text{B.}$ 若 $\int_0^x f(t) d t$ 在 $x=0$ 处可导,则 $f(x)$ 在 $x=0$ 处可导
$\text{C.}$ 若 $f^{\prime}(0)$ 存在,则 $f^{\prime}(0)$ 不一定等于 $\lim _{x \rightarrow 0} f^{\prime}(x)$
$\text{D.}$ 若 $f^{\prime}(0)$ 存在,则极限 $\lim _{x \rightarrow 0} \frac{f(x)-f(0)}{x^{\frac{1}{3}}}=0$
方程 $\ln \left(1+x+\frac{x^2}{2}\right)=x+k(\quad)$ .
$\text{A.}$ 没有根
$\text{B.}$ 恰有一个根
$\text{C.}$ 至少有两个根
$\text{D.}$ 根的个数与 $k$ 的取值有关
已知函数 $y=y(x)$ 由 $\left\{\begin{array}{l}x=\ln \left(1+ e ^{-2 t}\right), \\ y=2 t+\arctan e ^{-t}\end{array}\right.$ 确定,当 $x < \ln 2$ 时,函数 $y=y(x)(\quad)$ .
$\text{A.}$ 单调递增,且图形是凹的
$\text{B.}$ 单调递增,且图形是凸的
$\text{C.}$ 单调递减,且图形是凹的
$\text{D.}$ 单调递减,且图形是凸的
已知 $f(0)=-1$ ,导数 $f^{\prime}(x)$ 在 $[-5,3]$ 上连续,曲线 $y=f^{\prime}(x)$ 与直线 $x=-5, x=3$ 及 $x$轴围成的图像如图所示,相应的面积分别为 $S_1=2, S_2=4, S_3=3$ ,记 $f(x)$ 在 $[-5,3]$ 上的最大值为 $M$ ,最小值为 $m$ ,则 $M-m=(\quad)$ .
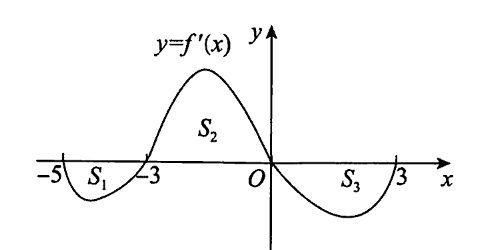
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
微分方程 $y^{\prime \prime \prime}+y^{\prime \prime}-2 y=3^x+x e ^{-x} \cos x$ ,下列 $a, b, b_1, b_2, c, c_1, c_2, d$ 均为任意常数,则其特解形式为( )。
$\text{A.}$ $a \cdot 3^x+x e ^{-x}\left[\left(b_1 x+c_1\right) \cos x+\left(b_2 x+c_2\right) \sin x\right]$
$\text{B.}$ $e \cdot 3^x+ e ^{-x}[(a x+b) \cos x+(c x+d) \sin x]$
$\text{C.}$ $a \cdot 3^x+x e ^{-x}(b x+c) \cos x$
$\text{D.}$ $3^x+ e ^{-x}[(a x+b) \cos x+(c x+d) \sin x]$
已知区域 $D$ 由曲线 $y=\sqrt{2 x-x^2}, y=\sqrt{2 x}$ 与直线 $x=2$ 围成,函数 $f(x, y)$ 在 $D$ 上连续,则对于二重积分 $\iint_D f(x, y) d x d y$ ,下列表达式错误的是( )。
$\text{A.}$ $\int_0^2 d x \int_{\sqrt{2 x-x^2}}^{\sqrt{2 x}} f(x, y) d y$
$\text{B.}$ $\int_0^1 d y \int_{\frac{y^2}{2}}^{1-\sqrt{1-y^2}} f(x, y) d x+\int_0^1 d y \int_{1+\sqrt{1-y^2}}^2 f(x, y) d x+\int_1^2 d y \int_{\frac{y^2}{2}}^2 f(x, y) d x$
$\text{C.}$ $\int_0^{\frac{\pi}{4}} d \theta \int_{2 \cos \theta}^{\frac{2}{\cos \theta}} f(r \cos \theta, r \sin \theta) r d r+\int_{\frac{\pi}{4}}^{\frac{\pi}{2}} d \theta \int_{2 \cos \theta}^{\frac{2 \cos \theta}{\sin ^2 \theta}} f(r \cos \theta, r \sin \theta) r d r$
$\text{D.}$ $\int_0^{\frac{\pi}{4}} d \theta \int_0^{\frac{2}{\cos \theta}} f(r \cos \theta, r \sin \theta) r d r+\int_{\frac{\pi}{4}}^{\frac{\pi}{2}} d \theta \int_{\frac{2}{\sin \theta}}^{\frac{2 \cos \theta}{2} \theta} f(r \cos \theta, r \sin \theta) r d r-\int_0^{\frac{\pi}{2}} d \theta \int_0^{2 \cos \theta} f(r \cos \theta, r \sin \theta) r d r$
已知 3 阶矩阵 $A , B$ 满足 $A B + A - B = E$ ,其中 $A =\left(\begin{array}{lll}1 & 3 & 2 \\ 2 & 2 & 1 \\ 4 & 3 & a\end{array}\right)$ ,且 $B \neq- E$ ,若齐次线性方程组 $( A + B ) x = 0$ 有唯一解,则常数 $a=(\quad)$ 。
$\text{A.}$ $\frac{11}{3}$
$\text{B.}$ 3
$\text{C.}$ -3
$\text{D.}$ 2
下列说法错误的是( ).
$\text{A.}$ 已知线性无关的向量组 $\alpha _1, \alpha _2, \cdots, \alpha _m$ 能由 $\beta _1, \beta _2, \cdots, \beta _n$ 线性表示,则存在某个向量 $\beta _i(1 \leqslant$ $i \leqslant n)$ ,使得 $\alpha _1, \alpha _2, \cdots, \alpha _{n-1}, \beta _i$ 线性无关
$\text{B.}$ 已知向量组 $\alpha _1, \alpha _2, \cdots, \alpha _m$ 的任意 $k$ 个向量均线性无关,且 $r\left( \alpha _1, \alpha _2, \cdots, \alpha _m\right)=k$ ,若 $l_1 \alpha _1+$ $l_2 \alpha _2+\cdots+l_m \alpha _m= 0$ ,则 $l_i(1 \leqslant i \leqslant m)$ 全为零或者至少有 $k+1$ 个系数不为零
$\text{C.}$ 任一矩阵 $A$ 中,位于线性无关行向量组与线性无关列向量组交叉处的子式一定不为零
$\text{D.}$ 向量组 $\alpha _1, \alpha _2, \cdots, \alpha _m$ 中存在 $k$ 个向量可表示任一 $\alpha _i(1 \leqslant i \leqslant m)$ ,且表示法唯一,则向量组 $\alpha _1, \alpha _2, \cdots, \alpha _m$ 的秩为 $k$
已知 5 阶可逆矩阵 $A$ 满足 $A ^{ T }= A ^*$ ,则 $\left| A ^2+2 A -3 E \right|=(\quad)$ .
$\text{A.}$ -1
$\text{B.}$ 0
$\text{C.}$ 1
$\text{D.}$ 2
填空题 (共 6 题 ),请把答案直接填写在答题纸上
已知函数 $f(x)$ 有任意阶导数,满足 $f^{\prime \prime}(x)-2 f(x)=x^{2021} \cos x$ ,其中 $f(0)=1, f^{\prime}(0)=$ 0 ,则 $f^{(2023)}(0)=$
若函数 $f(x)$ 连续,且满足 $f(x+l)=f(x), l>0$ ,则 $\int_{-l}^l f(x) \cos \frac{(2 n+1) \pi x}{l} d x=$
曲线 $y=\tan x\left(0 \leqslant x \leqslant \frac{\pi}{4}\right)$ 绕 $x$ 轴旋转一周所得旋转曲面的面积为
已知函数 $z=f(x, y)$ 满足 $r \cdot z_r^{\prime}=y, z_\theta^{\prime}=x$ ,其中 $\left\{\begin{array}{l}x=r \cos \theta, \\ y=r \sin \theta,\end{array}\right.$ 则 $z_x^{\prime}-z_y^{\prime}=$
已知区域 $D$ 由曲线 $L:\left(x^2+y^2\right)^2=x^2-y^2$ 的右半支围成,则 $\int_D x d \sigma=$
已知 $P _1=\left(\begin{array}{llll}0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{array}\right), P _2=\left(\begin{array}{llll}1 & 0 & 0 & 0 \\ 2 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{array}\right), B =\left(\begin{array}{llll}0 & 0 & 0 & 1 \\ 0 & 0 & 2 & 0 \\ 2 & 3 & 0 & 0 \\ 3 & 5 & 0 & 0\end{array}\right)$ 满足 $\left( P _1^{-1}\right)^5 A \left( P _2^{-1}\right)^2= B$ ,则 $A ^*=$
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
求极限 $\lim _{x \rightarrow+\infty}\left\{\int_0^1[a t+b(1-t)]^{\frac{1}{x}} d t+\frac{1}{x^2} \int_0^x t f(t) d t\right\}^x$ ,其中 $0 < b < a, \lim _{x \rightarrow+\infty} f(x)=0$ ,且反常积分 $\int_0^{+\infty} f(t) d t$ 收敛.
计算不定积分 $\int \frac{x}{\sqrt{a^2-x^2}} \ln \frac{\sqrt{a+x}}{2 a-x} d x(a>0)$ .
已知一长度为 $2 l$ ,线密度为 $\rho$ 的均匀细棒,另有一质量为 $m$ ,长度为 $2 l$ 的细杆与细棒一端垂直,且棒与杆相邻两端点的距离为 $l$ ,则细棒对细杆的引力为多少?( $G$ 为引力常量)
已知 $z(u, v)$ 具有二阶连续偏导数,自变量代换 $\left\{\begin{array}{l}u=x+a y, \\ v=x-2 y\end{array}\right.$ 使得
$$
6 \frac{\partial^2 z}{\partial x^2}+\frac{\partial^2 z}{\partial x \partial y}-\frac{\partial^2 z}{\partial y^2}=2 \frac{\partial z}{\partial x}+\frac{\partial z}{\partial y}
$$
化为不含 $\frac{\partial^2 z}{\partial u^2}$ 但含 $\frac{\partial^2 z}{\partial u \partial v}$ 的方程.
(1)求常数 $a$ ;
(2)求函数 $z(u, v)$ 的表达式.
已知 $f(x, y)=\left\{\begin{array}{ll}\frac{x}{\sqrt{4 x-x^2}}, & 2 x^2-4 x>y^2, \\ x(y+1), & 2 x^2-4 x < y^2,\end{array}\right.$ 求二重积分 $\iint_D f(x, y) d x d y$ ,其中区域 $D$ 由直线 $x=4$ 与曲线 $x=4-\sqrt{16-y^2}$ 围成.
已知矩阵 $A =\left(\begin{array}{ccc}2 & 3 & 2 \\ 1 & 4 & 2 \\ 1 & -3 & a\end{array}\right)$ 与矩阵 $B =\left(\begin{array}{ccc}3 & 0 & 0 \\ c & 3 & 0 \\ 2 & 0 & b\end{array}\right)$ 相似.
(1)求参数 $a, b$ ;
(2)求可逆矩阵 $P$ ,使得 $P ^{-1} A P = B$ .