单选题 (共 8 题 ),每题只有一个选项正确
集合 $A=\left\{0,2, x^2+1\right\}, B=\{0, x+3\}$ ,若 $A \cap B=B$ ,则 $x=$
$\text{A.}$ -1
$\text{B.}$ 0
$\text{C.}$ 2
$\text{D.}$ -1 或 2
若关于 $x$ 的不等式 $a x^2-a x-1 \geqslant 0$ 的解集为空集,则 $a$ 的取值范围是
$\text{A.}$ $(-4,0)$
$\text{B.}$ $[-4,0]$
$\text{C.}$ $(-4,0]$
$\text{D.}$ $[-4,0)$
复数 $z$ 的模为 13 ,实部为 5 ,则 $z \cdot i=$
$\text{A.}$ $\pm 12+5 i$
$\text{B.}$ $\pm 12-5 i$
$\text{C.}$ $12 \pm 5 i$
$\text{D.}$ $-12 \pm 5 i$
若函数 $f(x)=\frac{2 \sqrt{3} \sin ^2 \omega x+\sin 2 \omega x-\sqrt{3}}{2 \cos ^2 \omega x+2 \sqrt{3} \sin \omega x \cos \omega x-1}$ 的最小正周期为 1 ,则 $\omega=$
$\text{A.}$ $\frac{\pi}{2}$
$\text{B.}$ $\pi$
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ 1
已知函数 $f(x)=\frac{ e ^x-1}{ e ^x+1}-\cos \left(x+\frac{\pi}{2}\right)+3$ ,若 $f\left(x_0\right)=-1$ ,则 $f\left(-x_0\right)=$
$\text{A.}$ 1
$\text{B.}$ 3
$\text{C.}$ 5
$\text{D.}$ 7
正方体 $A B C D-A_1 B_1 C_1 D_1$ 中,$E, ~ F, ~ G$ 分别是 $A B, ~ C C_1, ~ C_1 D_1$ 的中点,则
$\text{A.}$ 直线 $A G$ 与 $E F$ 是平行直线
$\text{B.}$ 过 $E, ~ F, ~ G$ 三点的平面与正方体的截面是六边形
$\text{C.}$ 直线 $E F$ 与平面 $A B C D$ 所成角的正切值是 $\frac{\sqrt{3}}{3}$
$\text{D.}$ 若正方体的棱长为 2 ,则点 $B$ 到平面 $B_1 E F$ 的距离是 $\frac{2 \sqrt{21}}{21}$
离散型随机变量 $X$ 的分布列如下:
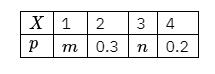
若 $E(X)=2.7$ ,则下列结论错误的是
$\text{A.}$ $m+n=0.5$
$\text{B.}$ $E(3 X-1)=7.1$
$\text{C.}$ $D(X)=0.81$
$\text{D.}$ $P(X>2)=0.5$
已知双曲线 C:$x^2-\frac{y^2}{3}=1$ ,直线 $l$ 过点 $(0,1)$ ,以下正确的是
$\text{A.}$ 若直线 $l$ 与双曲线 $C$ 只有一个公共点,则直线 $l$ 的条数是 2
$\text{B.}$ 若直线 $l$ 与双曲线 $C$ 只有一个公共点,则直线 $l$ 的斜率是 $\frac{1}{2}$ 或 $\pm 2$
$\text{C.}$ 若直线 $l$ 与双曲线 $C$ 有两个不同的公共点,则直线 $l$ 的斜率范围是 $(-2,2)$
$\text{D.}$ 若直线 $l$ 与双曲线 $C$ 的渐近线相交于 $A, ~ B$ 两点,则线段 $A B$ 中点的轨迹是直线
多选题 (共 3 题 ),每题有多个选项正确
已知在首项为 1,公差为 $d$ 的等差数列 $\left\{a_n\right\}$ 中,$a_1, ~ a_2, ~ a_6$ 是等比数列 $\left\{b_n\right\}$ 的前三项,数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$ ,则
$\text{A.}$ $d=0$ 或 $d=3$
$\text{B.}$ $S_n=\frac{n(2 n-1)}{2}$
$\text{C.}$ $\left\{\frac{S_n}{n}\right\}$ 是等差数列
$\text{D.}$ $b_n=4^{n-1}$
过抛物线 $y^2=4 x$ 的焦点 $F$ 的直线与抛物线相交于 $A, B$ 两点,且 $\overrightarrow{A F}=2 \overrightarrow{F B}$ ,则
$\text{A.}$ $|A B|=\frac{9}{2}$
$\text{B.}$ 直线 $A B$ 的斜率为 $\pm \frac{\sqrt{2}}{4}$
$\text{C.}$ 以 $A B$ 为直径的圆与直线 $x=a$ 相切,则 $a=-1$ 或 $a=\frac{7}{2}$
$\text{D.}$ 抛物线上 $A, B$ 两点处的切线互相垂直
已知 $f(x)=\frac{1}{2} x^2, g(x)=\ln x$ ,则下列说法正确的是
$\text{A.}$ 曲线 $y=f(x)$ 与 $y=g(x)$ 有公共点
$\text{B.}$ 曲线 $y=g(x)$ 关于直线 $y=x$ 对称的曲线是 $y= e ^x$
$\text{C.}$ 曲线 $y=f(x)$ 关于直线 $y=-x$ 对称的曲线是 $y^2=-2 x$
$\text{D.}$ 直线 $x=t(t>0)$ 与曲线 $y=f(x), y=g(x)$ 的交点分别是 $A, B$ ,则 $|A B|$ 的最小值为 $\frac{1}{2}$
填空题 (共 3 题 ),请把答案直接填写在答题纸上
正六边形 $A B C D E F$ 的边长为 1,则 $\overrightarrow{A B} \cdot \overrightarrow{A C}+\overrightarrow{A C} \cdot \overrightarrow{A D}+\overrightarrow{A D} \cdot \overrightarrow{A B}=$
在 $x+\frac{1}{2 x}{ }^n$ 的展开式中,仅第 5 项的二项式系数最大,则展开式中系数最大的项是
已知圆锥 $S O$ 的底面半径为 2 ,体积为 $\frac{16}{3} \pi, A B C D E$ 是底面圆 $O$ 的内接五边形,则五棱锥 $S-A B C D E$ 的外接球的表面积为
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
$\triangle A B C$ 中,角 $A, ~ B, ~ C$ 的对边分别是 $a, ~ b, ~ c$ ,且 $b^2+c^2-a^2=-2 b c \sin A$ .
(1)求角 $A$ ;
(2)点 $D$ 在 $B C$ 边上,且 $\overrightarrow{B D}=2 \overrightarrow{D C}, A D=2$ ,求 $\triangle A B C$ 面积的最大值.
在三棱锥 $P-A B C$ 中,平面 $P A C \perp$ 平面 $A B C, \triangle P A C$ 是边长为 2 的正三角形,$A B=2, B C=2 \sqrt{2}$ .
(1)证明:$A B \perp P C$ ;
(2)求二面角 $P-B C-A$ 的余弦值.
已知函数 $f(x)=a \ln x-x-1, a \in R$ .
(1)讨论 $f(x)$ 的单调性;
(2)$n$ 为正整数,当 $a=1$ 时,曲线 $y=f(x)$ 在点 $(n, f(n))$ 处的切线记为 $L_n$ ,直线 $L_n$ 与 $y$ 轴交点的纵坐标记为 $y_n$ ,证明:$y_1+y_2+y_3+\cdots+y_n \leq \frac{n^2-5 n}{2}$ .
椭圆 $C$ 的中心在坐标原点,对称轴是坐标轴,点 $P\left(1, \frac{3}{2}\right)$ 和点 $Q\left(-\frac{2 \sqrt{3}}{3}, \sqrt{2}\right)$
在椭圆 $C$ 上.
(1)求椭圆 $C$ 的方程;
(2)$A, B$ 是椭圆 $C$ 的左,右顶点,过点 $(-1,0)$ 的直线 $l$ 与椭圆 $C$ 相交于 $M, N$ 两点(不与 $A$ , $B$ 重合),直线 $A M$ 与直线 $B N$ 相交于点 $G$ ,求证:点 $G$ 在一条定直线上.
为贯彻落实《全民健身条例》,进一步推动羽毛球运动发展,某市举办"北江杯"羽毛球团体赛,第一阶段是分组循环赛,每组前两名出线进行第二阶段的交叉淘汰赛。某小组有甲,乙,丙,丁四支队伍,每支队伍派出 5 对双打(三对男双,一对女双,一对混双)进行比赛,出场顺序抽签决定,每场比赛结果互不影响,先胜三场的队伍获胜并结束比赛(俗称"见三收")。在甲,乙两支队伍的比赛中,甲队伍中混双 $M$ 的胜率是 $\frac{2}{3}$ ,其余 4 对双打的胜率均是 $\frac{1}{2}$ .
(1)混双 $M$ 在前 4 场中没有比赛的前提下,求甲队伍在前 4 场比赛结束就获胜的概率;
(2)求甲队伍在前 3 场比赛结束就获胜的概率;
(3)若甲队伍在前 3 场比赛结束就获胜,求混双 $M$ 在前 3 场中有比赛的概率.