单选题 (共 8 题 ),每题只有一个选项正确
若命题 $p: \forall x>1, x^2-3 x+2>0$ ,则
$\text{A.}$ $p$ 是真命题,且 $\neg p: \exists x>1, x^2-3 x+2 \leqslant 0$
$\text{B.}$ $p$ 是真命题,且 $\neg p: \exists x \leqslant 1, x^2-3 x+2 \leqslant 0$
$\text{C.}$ $p$ 是假命题,且 $\neg p: \exists x>1, x^2-3 x+2 \leqslant 0$
$\text{D.}$ $p$ 是假命题,且 $\neg p: \exists x \leqslant 1, x^2-3 x+2 \leqslant 0$
在复平面内,复数 $z$ 对应的点与 $\frac{1+ i }{2+ i }$ 对应的点关于实轴对称,则 $z=$
$\text{A.}$ $\frac{3}{5}+\frac{1}{5} i$
$\text{B.}$ $\frac{3}{5}-\frac{1}{5} i$
$\text{C.}$ $-\frac{3}{5}+\frac{1}{5} i$
$\text{D.}$ $-\frac{3}{5}-\frac{1}{5} i$
已知角 $\alpha$ 满足 $\sin \left(\alpha-10^{\circ}\right)=\frac{1}{5}$ ,则 $\cos \left(\alpha+260^{\circ}\right)=$
$\text{A.}$ $-\frac{2 \sqrt{6}}{5}$
$\text{B.}$ $\frac{2 \sqrt{6}}{5}$
$\text{C.}$ $-\frac{1}{5}$
$\text{D.}$ $\frac{1}{5}$
已知 $x=1$ 是函数 $f(x)=\ln x-\frac{a}{x}+x$ 的极值点,则 $a=$
$\text{A.}$ 2
$\text{B.}$ -2
$\text{C.}$ 1
$\text{D.}$ -1
已知随机变量 $X \sim B\left(n, \frac{2}{3}\right), Y \sim N\left(4, \sigma^2\right)$ ,且 $P(-1 \leqslant Y \leqslant 4)+P(Y>n)=0.5$ ,则 $E(X)=$
$\text{A.}$ 2
$\text{B.}$ 4
$\text{C.}$ 6
$\text{D.}$ 8
将函数 $f(x)=\sqrt{3} \sin 2 x-\cos 2 x$ 图象上所有点的横坐标变为原来的 $\frac{1}{\omega}(\omega>0)$ ,纵坐标不变,得到函数 $g(x)$ 的图象,若 $g(x)$ 在 $\left(0, \frac{\pi}{3}\right)$ 上单调,则 $\omega$ 的取值范围为
$\text{A.}$ $(0,1]$
$\text{B.}$ $\left(0, \frac{1}{2}\right]$
$\text{C.}$ $[1,+\infty)$
$\text{D.}$ $\left[\frac{1}{2},+\infty\right)$
由阿基米德的著作《关于圆锥体和球体》可知,椭圆的面积等于圆周率 $\pi$ 与椭圆的长半轴长和短半轴长的乘积.已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的离心率为 $\frac{5 \sqrt{2}}{8}, F_1, F_2$ 分别为 $C$ 的左、右焦点,$C$ 上一点 $P$ 满足 $\overrightarrow{P F_1} \cdot \overrightarrow{P F_2}=0$ ,且 $\triangle P F_1 F_2$ 的面积为 $\frac{7}{2}$ ,则 $C$ 的面积为
$\text{A.}$ $\sqrt{7} \pi$
$\text{B.}$ $2 \sqrt{7} \pi$
$\text{C.}$ $\sqrt{14} \pi$
$\text{D.}$ $2 \sqrt{14} \pi$
已知函数 $f(x)$ 的定义域为 $(0,+\infty)$ ,对于任意的 $y>x>0$ ,都有 $x f(y)-y f(x)+x^2 y-$ $x y^2>0$ .若 $f(4)=4$ ,且 $f(x+a) < x^2+(2 a-3) x+a^2-3 a$ 在 $x \in[1,4]$ 时恒成立,则 $a$ 的取值范围为
$\text{A.}$ $(-1,0)$
$\text{B.}$ $(-1,4)$
$\text{C.}$ $(0,+\infty)$
$\text{D.}$ $(4,+\infty)$
多选题 (共 3 题 ),每题有多个选项正确
已知抛物线 $C: y^2=2 p x(p>0)$ 的焦点为 $F$ ,过 $F$ 且斜率为 1 的直线 $l$ 与 $C$ 交于 $A, B$ 两点,若 $|A B| < 8$ ,则 $p$ 的值可能为
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ 1
$\text{C.}$ $\frac{3}{2}$
$\text{D.}$ 2
如图,在直三棱柱 $A B C-D E F$ 中,$A D=A B=B C=2, A B \perp B C, M$ 为 $A D$ 的中点,则
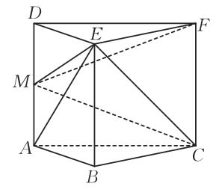
$\text{A.}$ $M E \perp E C$
$\text{B.}$ 三棱锥 F-MEC 的体积为 $\frac{4}{3}$
$\text{C.}$ 直线 $M E$ 与 $A C$ 所成角的余弦值为 $\frac{\sqrt{10}}{5}$
$\text{D.}$ 三棱锥 $E-A B C$ 的外接球的表面积为 $4 \sqrt{3} \pi$
设集合 $A=\left\{ a \mid a =\left(a_1, a_2, a_3\right), a_1, a_2, a_3 \in R \right\}$ ,且 $\forall x \in R , a =\left(a_1, a_2, a_3\right) \in A, b =\left(b_1\right.$ , $\left.b_2, b_3\right) \in A, a + b =\left(a_1+b_1, a_2+b_2, a_3+b_3\right), x a =\left(x a_1, x a_2, x a_3\right)$ 。定义运算 $\|\|$ :若满足 (1)$\forall a \in A,\| a \| \geqslant 0$ ,且当且仅当 $a =(0,0,0)$ 时,$\| a \|=0$ ,(2)$\forall a \in A, x \in R ,\|x a \|=|x| \cdot\| a \|$ , (3)$\forall a , b \in A,\| a + b \| \leqslant\| a \|+\| b \|$ 这三个条件,则称 $\|\|$ 为 $A$ 上的范数.下列结论正确的是
$\text{A.}$ 若 $\|\|$ 为 $A$ 上的范数,且 $\exists x, y \in R , a , b \in A\|, x a +y b \|=0$ ,则 $x=y=0$
$\text{B.}$ 若 $\|\|$ 为 $A$ 上的范数,则 $\forall x, y \in R , a , b \in A\|, x a +y b \|\leqslant|x| \cdot\| a \|+|y| \cdot\| b \|$
$\text{C.}$ 定义运算 $\lceil\quad\rceil: \forall a =(x, y, z) \in A,\lceil a \rceil=(\sqrt[3]{x}+\sqrt[3]{y}+\sqrt[3]{z})^3$ ,则 $\lceil\quad\rceil$ 为 $A$ 上的范数
$\text{D.}$ 定义运算 $L \quad \downarrow: \forall a =(x, y, z) \in A,\lfloor a \rfloor=\sqrt{x^2+y^2+z^2}$ ,则 $L \quad$ 为 $A$ 上的范数
填空题 (共 3 题 ),请把答案直接填写在答题纸上
若圆 $C: x^2+y^2+2 x+m=0$ 上恰有三个不同的点到直线 $l: x+\sqrt{3} y+2=0$ 的距离为 1 ,则 $m=$
已知 $O$ 为坐标原点,直线 $x=m(0 < m < e )$ 与函数 $f(x)=\frac{\ln x}{ e }, g(x)=\frac{1}{x}$ 的图象分别交于 $M, N$ 两点,则 $\triangle O M N$ 面积的最大值为
如图,在 $1 \times 9$ 的格子中,数字 $1,2, \cdots, 9$ 从左到右为升序排列,现在用计算机随机生成一个整数 $a$ ,若 $a$ 为奇数,则将格子中数字 1 和 9 的位置互换, 3 和 7 的位置交换,其余位置不变;若 $a$ 为偶数,则将格子中数字 2 和 8 的位置互换, 4 和 6 的位置交换.设电脑随机生成 $n\left(n \in N ^*\right)$ 个数字后, $1 \times 9$ 格子中的数字恰好从左到右为降序排列的概率为 $P_n$ ,则 $P_n$ $=$

解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
某地为了探索中小学人工智能教育实施的有效途径,了解中小学生使用 AI 工具的情况,随机地对 100 名中学生和 100 名小学生进行调查,其中有 120 人经常使用 AI 工具辅助学习,若在不经常使用 AI 工具辅助学习的学生中按比例用分层随机抽样的方法抽取 4 人,则小学生有 3 人被选中。
(1)根据题中信息,完成下面列联表:
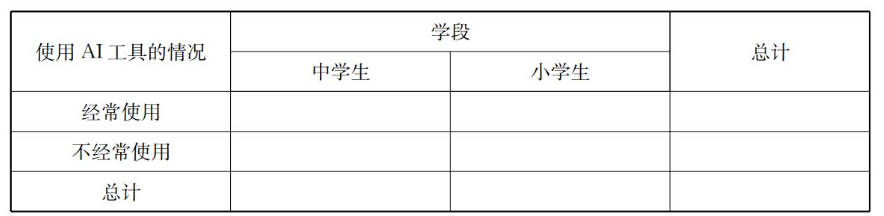
(2)根据(1)中的列联表,判断是否有 $99.9 \%$ 的把握认为学生使用 AI 工具的情况与学段有关.
$\triangle A B C$ 的内角 $A, B, C$ 的对边分别为 $a, b, c$ ,已知 $a \sin (C-B)=b \sin (A-C)$ .
(1)若 $C=2 B$ ,求 $A$ 的值;
(2)求 $C$ 的最大值.
已知数列 $\left\{a_n\right\},\left\{b_n\right\}$ 满足 $b_n=a_n+a_{n+1}+\cdots+a_{2 n}$ .
(1)若 $a_n=2^n$ ,求 $b_1-b_2+b_3$ 的值.
(2)若 $a_n=n$ ,证明:$\frac{1}{b_1}+\frac{1}{b_2}+\cdots+\frac{1}{b_n} < \frac{2}{3}$ .
(3)若 $b_n=3 n^2+2 n-1$ ,设 $c_n=a_n-2 n+1$ ,证明:$c_{2 n+1}+c_{2 n+2}=c_n$ 。
已知函数 $f(x)=x^2+\frac{1}{x}-2 e ^{1-x}(x>0)$ .
(1)求 $f(x)$ 的图象在点 $(1, f(1))$ 处的切线方程;
(2)求 $f(x)$ 的零点个数;
(3)证明:$f(x) \geqslant 3 \ln x$ .
在平面直角坐标系 $x O y$ 中,将双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 绕着 $y$ 轴旋转一周构成双曲面 $D$ ,其中 $C$ 在旋转过程中的所有实轴落在 $x O z$ 平面内,设 $x O z$ 所在的平面为 $\alpha$ ,平面 $\beta$满足 $\alpha / / \beta$ ,且 $\alpha$ 与 $\beta$ 之间的距离为 $\sqrt{3} b$ .
(1)若点 $P(x, z, y)$ 在 $D$ 上,试用含 $x, z, y$ 的方程表示 $D$(不用说明理由).
(2)设 $T_\alpha, T_\beta$ 分别是 $\alpha, \beta$ 截得 $D$ 的截面.
(i)设 $l_\alpha, l_\beta$ 分别为 $T_\alpha, T_\beta$ 上的弦,求 $l_\alpha, l_\beta$ 所在直线间的距离的取值范围;
(ii)已知截面 $T_\beta$ 的圆周上的点 $A_1, A_2, \cdots, A_n$ 恰好构成正 $n$ 边形的顶点,$P$ 为 $D$ 上一动点,若对任意 $a>b>0, \lambda\left|\sum_{i=1}^n \overrightarrow{P A_i}\right| \geqslant n \sqrt{a^2-b^2}$ 恒成立,求 $\lambda$ 的取值范围.