一、单选题 (共 2 题 ),每题只有一个选项正确
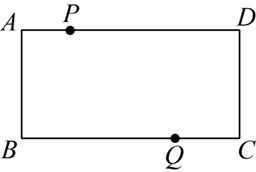
1. 如图,
、、、 分别是四边形
四条边的中点,顺次连接
、、、 得四边形
,连接
、
,下列命题不正确的是
当四边形 是矩形时,四边形 是菱形
当四边形 是菱形时,四边形 是矩形
当四边形 满足 时,四边形 是菱形
当四边形 满足 时,四边形 是矩形
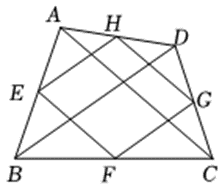
2. 如图 1,菱形
中,
,动点
以每秒 1 个单位的速度自点
出发沿线段
运动到点
,同时动点
以每秒 2 个单位的速度自点
出发沿折线
运动到点
.图 2 是点
、 运动时,
的面积
随时间
变化关系图象,则
的值是
2
2.5
3
二、解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
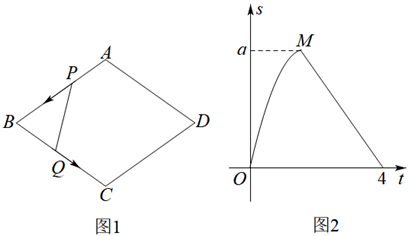
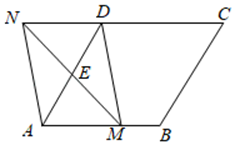
3. 如图,在四边形
中,
分别是
的中点,
分别是对角线
的中点,依次连接
,
,连接
.
(1)求证:四边形
是平行四边形;
(2)当
时,
与
有怎样的位置关系?请说明理由;
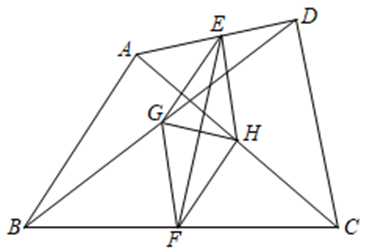
4. 如图,
、 是四边形
的对角线,点
、、、 分别是线段
、、、 上的中点
(1)求证:线段
、 互相平分;
(2)四边形
满足什么条件时,
?证明你得到的结论.
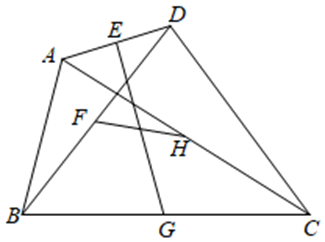
5. 已知:如图,四边形
四条边上的中点分别为
、、、 ,顺次连接
、、、 ,得到四边形
(即四边形
的中点四边形).
(1)四边形
的形状是
,请证明你的结论;
(2)当四边形
的对角线满足
条件时,四边形
是菱形;
(3)你学过的哪种特殊的平行四边形的中点四边形是菱形?请写出一种.
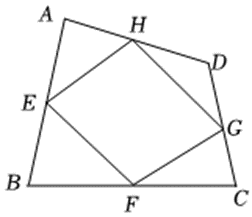
6. 如图,在菱形
中,
,点
是
边的中点.点
是
边上一动点 (不与点
重合),连接
并延长交
的延长线于点
,连接
、 .
(1)求证:四边形
是平行四边形;
(2)当
时,求证:四边形
是矩形;
(3)填空:当
的值为
时,四边形
是菱形.
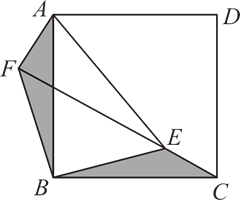
7. 如图,已知
是正方形
内一点,
,
.将
绕点
旋转
.连结
.
(1)直接写出
、 的长度和
的度数.
(2)求
的长.
(3)试判断
的形状并说明理由.
8. 如图,在矩形
中,
,点
在
边上以每秒 1 cm 的速度从点
向点
运动,点
在
边上,以每秒 4 cm 的速度从点
出发,在
之间往返运动,两个动点同时出发,当点
到达点
时停止(同时点
也停止运动),设运动时间为
秒
.
(1)用含
的式子表示线段的长度:
cm,
(2)当
时,运动时间
为
秒时,以
、、、 为顶点的四边形是矩形.
(3)当
时,以
、、、 为顶点的四边形有没可能是平行四边形?若有,请求出
;若没有,请说明理由.